How do you find the area between #y=x, y=2-x, y=0#?
1 Answer
Let
Explanation:
First, a good thing to do would be sketch the graph.
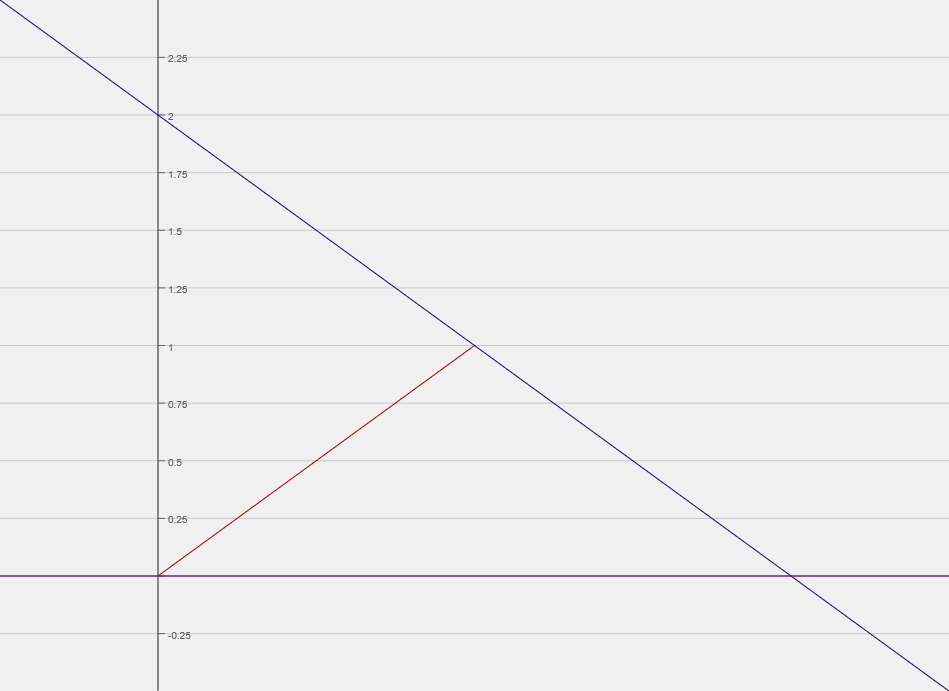
So, we are looking for the area of that triangle.
Take note of the points of intersection.
Here we are dealing with
So we set both equations equal and get
So, both functions intersect at
Since we are only dealing with values greater than
And since our area is bounded on the left by

