How do you find the area inside of the Cardioid #r = 2+2cosθ# and outside the circle r = 3?

Question

31006 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-05T07:36:57

#= 8 - (3 pi)/2#

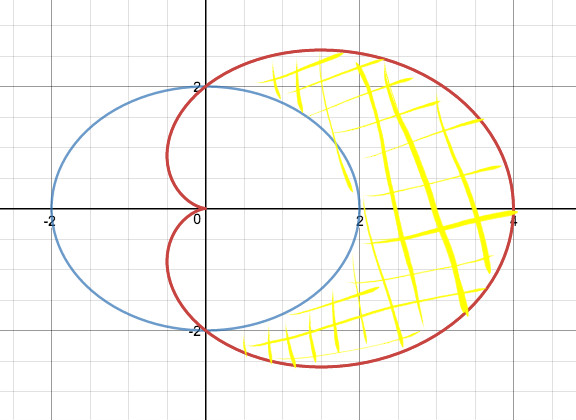
enter image source here

area in polar is #1/2 int_{theta 1}^ {theta 2} r^2(theta) d theta# .

due to symmetry, the shaded area is #2 times int_{0}^ {pi/2}#

which means
#A =2 times ( 1/2 int_0^{pi/2} (2 + 2 cos theta)^2 d theta- 1/2 int_0^{pi/2} 3^2 d theta)#

# = int_0^{pi/2} d theta qquad (2 + 2 cos theta)^2 - 9 #

# = int_0^{pi/2} d theta qquad 4 cos^2 theta + 8 cos theta - 5 #

# = int_0^{pi/2} d theta qquad 2 (cos2 theta + 1) + 8 cos theta - 5 #

# = int_0^{pi/2} d theta qquad 2 cos2 theta + 8 cos theta - 3 #

# = [sin 2 theta + 8 sin theta - 3theta ]_0^{pi/2}#

#= 8 - (3 pi)/2#