How do you find the area of the rectangle with vertices A(-5,1), B(-3,-1), C(3,5), D(1,7)?
1 Answer
Jul 8, 2016
Area
Explanation:
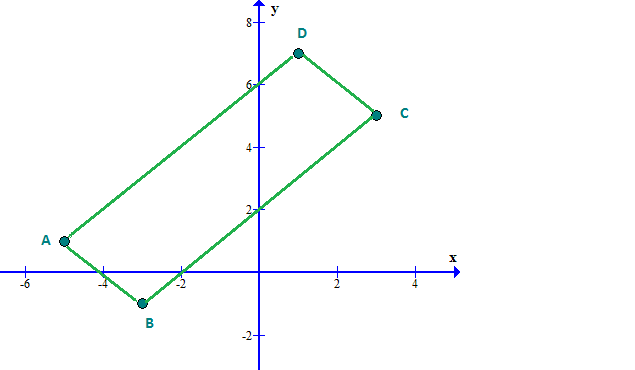
The area of
One would be to divide the rectangle into two triangles, then use the Pythagorean Theorem to find the distances between the points, and finally use Heron's formula to find the areas of the two triangles.
However, I think the method below is easier.
Enclose the rectangle
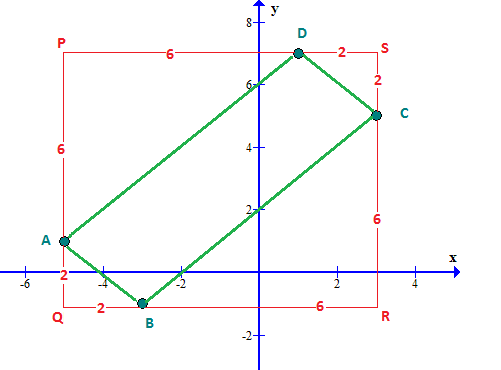
Therefore
