Question

How do you find the area of the region that lies inside the curves `r= 1+cos(theta)` and `r= 1-cos(theta)`?

Answer 1

First let us "see" our area:

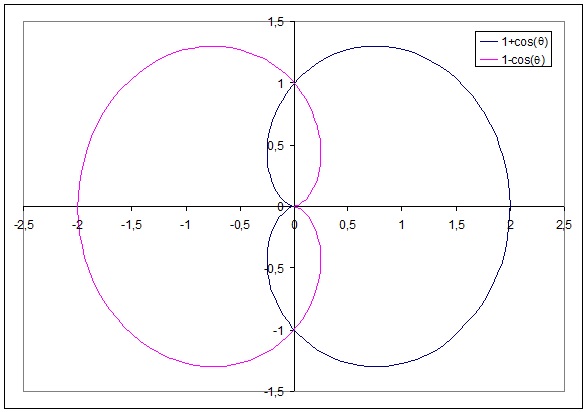
Basically you want the area of the two loops enclosed by the two curves (vertically along the vertical axis).

In general the area in polar form is:
`1/2int_(theta_1)^(theta_2)r^2d(theta)` (have a look to any maths book on calculus/analytical geometry).

In this case let us start with the upper loop; you have:

`0->pi/2` for the red line + `pi/2->pi` for the blue line
area red shaded + area blue shaded

Area1= `1/2int_0^(pi/2)(1-cos(theta))^2d(theta)+1/2int_(pi/2)^(pi)(1+cos(theta))^2d(theta)`
So you get:

Hope it helps (check my maths)