How do you find the area of the region that lies inside the polar graphs, #r = 1 - sin theta# and #r = sin theta#?
1 Answer
Feb 26, 2015
First let's have a look at our areas:
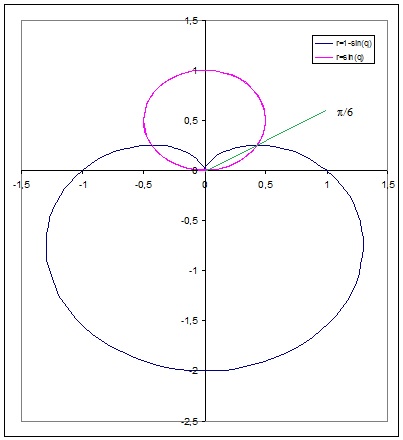
Basically we want the area of the two leafs like shapes at
By setting equal the two equations I get the inclination
In general the area in polar form is:
To find the area of the first leaf (Area 1) you have:
(area from the red curve to the green line)+(area from the green line to the blue curve)=
Area 1=

(Please, check my calculations)

