How do you find the area of the surface generated by rotating the curve about the y-axis #x^(2/3)+y^(2/3)=1# for the first quadrant?

Question

4652 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-23T21:02:20

#(6 pi)/5#

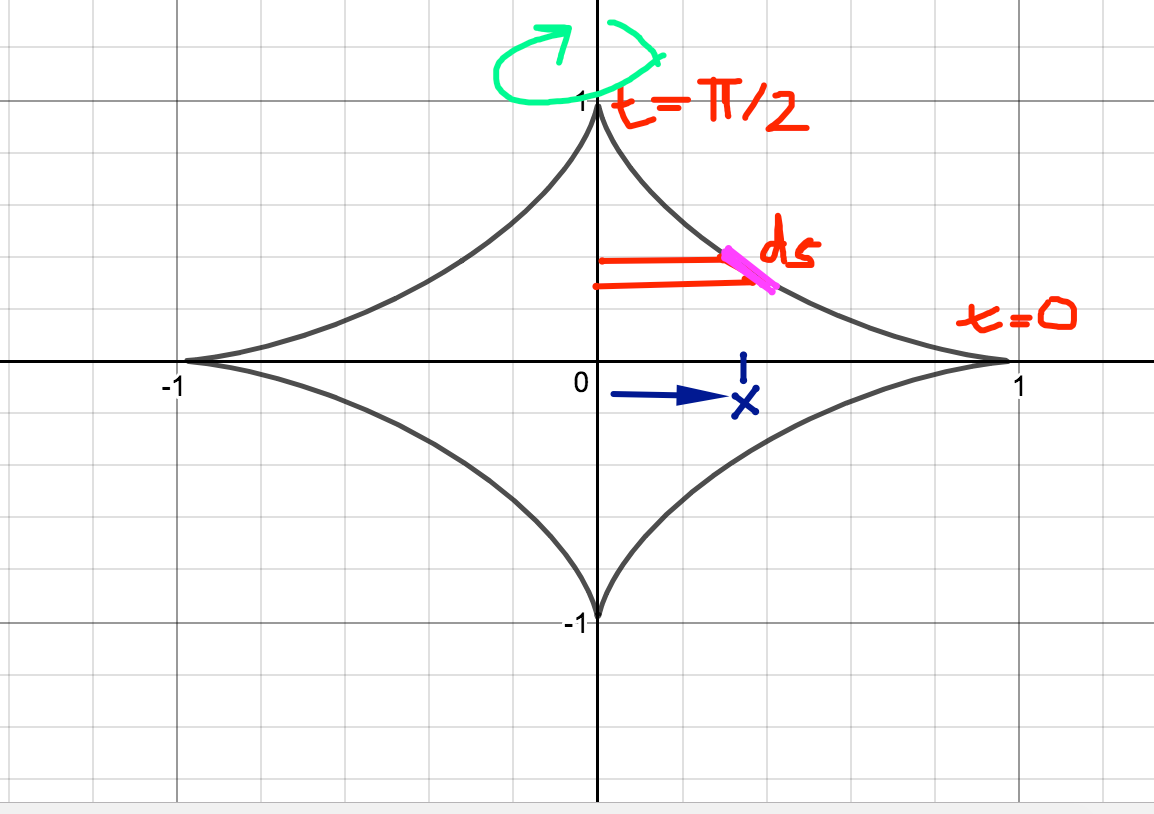
enter image source here

We can param this:

Let #x = cos^3 t# and #y = sin^3 t# so that we do indeed have #x^(2/3)+y^(2/3)=1#

Then arc lenth along the curve in Q1 is:

#ds = dot s \ dt = sqrt(dot x^2 + dot y ^2) \ dt#

#= sqrt((-3 cos^2 t sin t)^2 + (3 sin ^2 t cos t) ^2) \ dt#

# = 3 cos t sin t \ dt#

The surface area of the revolution around the y-axis is:

#dS = 2 pi x ds#

# = 6 pi \ cos^4 t \ sin t \ dt#

And:

#S = 6 pi \ int_(t = 0)^(pi/2) \ dt qquad cos^4 t \ sin t#

# = 6 pi (- 1/5cos^5 t)_(t = 0)^(pi/2) = (6 pi)/5#