How do you find the area of the trapezoid below?

1 Answer
Explanation:
The quick way of finding the area of this trapezoid would be to simply use the know formula, which looks like this
#color(blue)(A = (B + b)/2 * h)" "# , where
In this case, you have a trapezoid that has the longer base equal to
This means that you would get
#A = (20 + 18)/2 * 10 = 38/2 * 10 = color(green)(190)#
The more interesting way, assuming that you don't remember the formula, would be to try and find it "by hand", so to speak
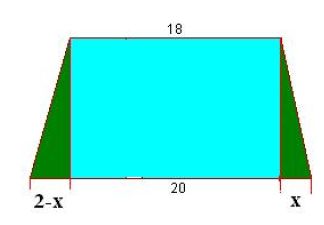
Notice that you can form the area of the trapezoid by adding the area of the central rectangle, shown in light blue, and the areas of the two right triangles, shown in forest green.
Now, the central rectangle will have the dimensions of the short base and of the height, i.e.
#A_"rectangle" = 18 * 10 = 180#
Now, you know that the difference between the long base and the short base is equal to
This means that if you use
#A_"left triangle" = 1/2 * (2-x) * 10#
and
#A_"right triangle" = 1/2 * x * 10#
This means that the total area of the trapezoid will be
#A = A_"left triangle" + A_"right triangle" + A_"rectangle"#
#A = 1/2(2-x) * 10 + 1/2 * x * 10 + 180#
#A = 10 - color(red)(cancel(color(black)(5x))) + color(red)(cancel(color(black)(5x))) + 180 = color(green)(190)#

