How do you find the asymptotes for (x^3-8)/(x^2-5x+6)?
1 Answer
Explanation:
First, we simplify the given function.
Factorize the numerator:
This is of the form
And we know that
Therefore,
Factorize the denominator:
The given equation is a quadratic equation, of the form:
Where,
This equation can be solved using the quadratic formula.
The step-by-step walk through to solving the quadratic equation is given here
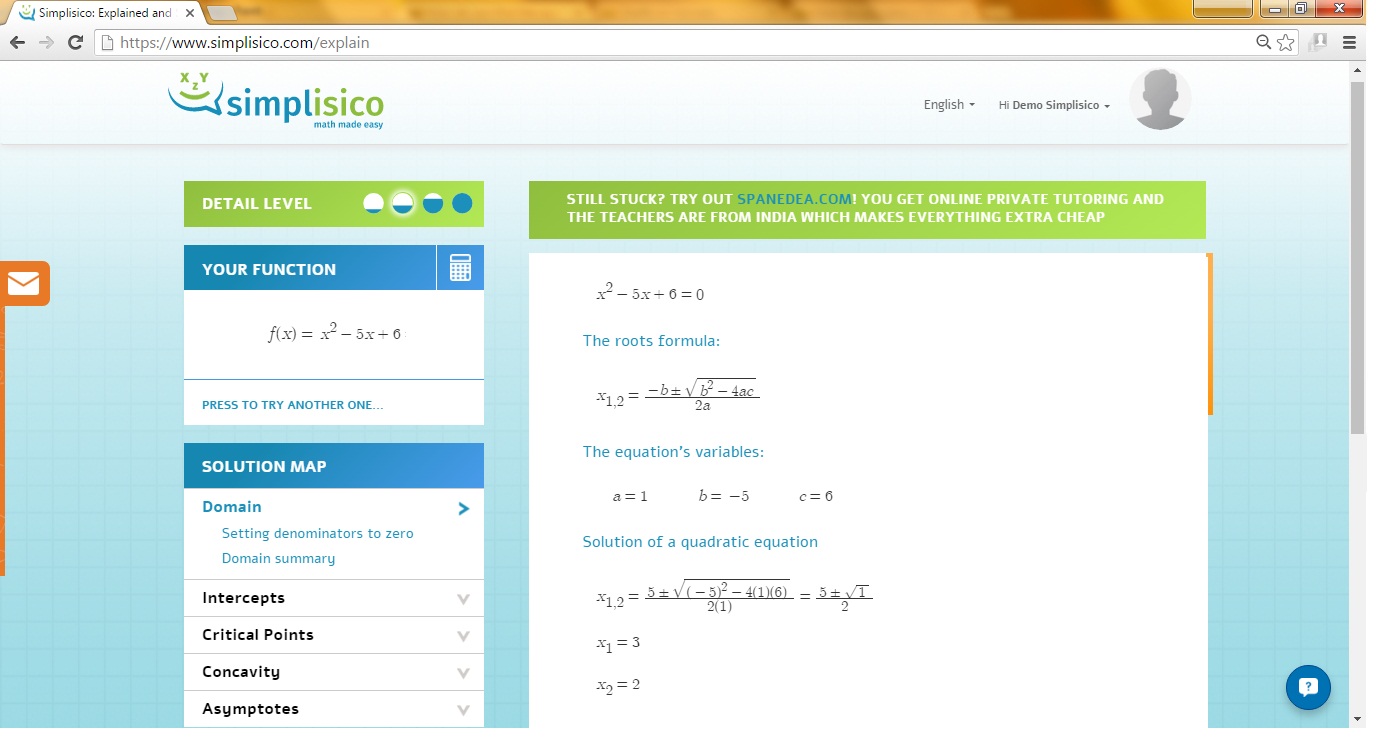
The factors are
Now rewriting the function as
Here,
Our function is now
Now we find the asymptotes.
An ASYMPTOTE is a line that approches a curve, but NEVER meets it.
To find the vertical asymptote , put the denominator = 0 (because 0 cannot divide any number) and solve.
Given below is the step-by-step walk through
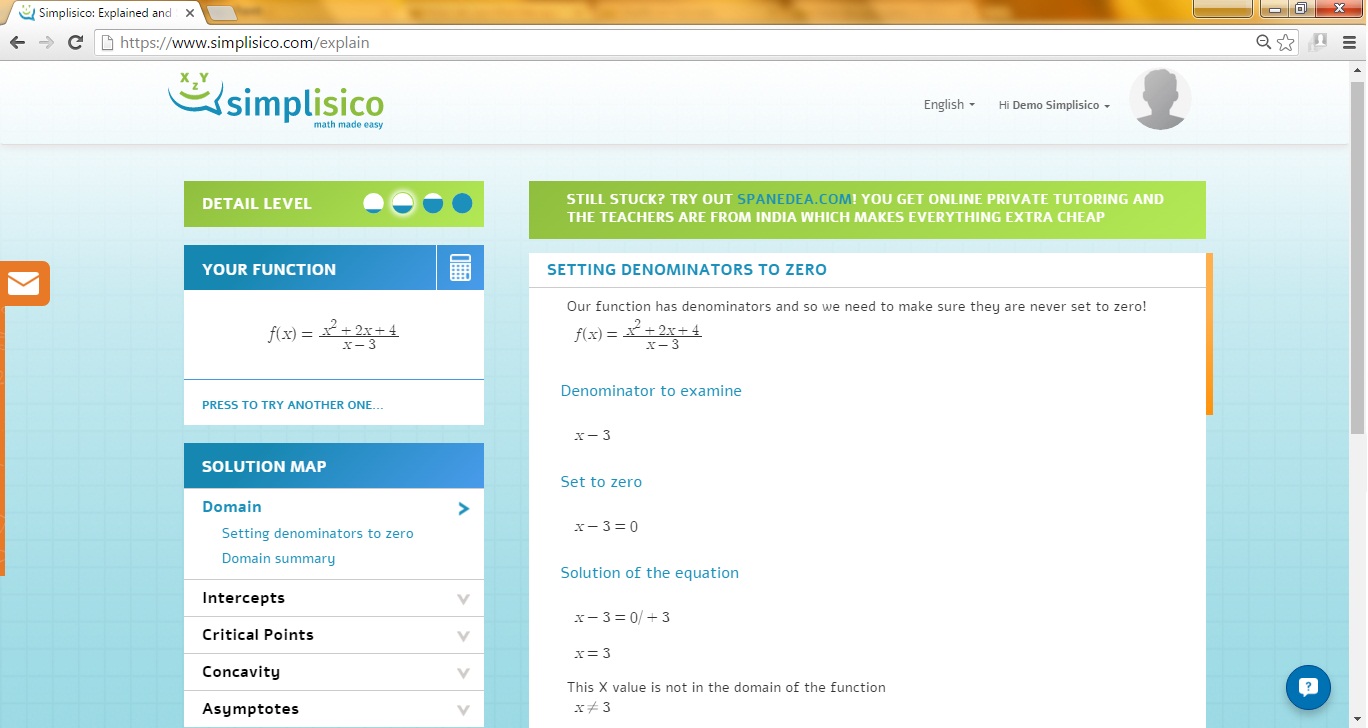
The curve will never touch the line
Next, we find the horizontal asymptote:
Compare the degree of the expressions in the numerator and the denominator.
Since the degree in the numerator is greater than the degree in the denominator, there are no horizontal asymptote.
The oblique asymptote is a line of the form y = mx + c.
Oblique asymtote exists when the degree of numerator = degree of denominator + 1
To find the oblique asymptote divide the numerator by the denominator.
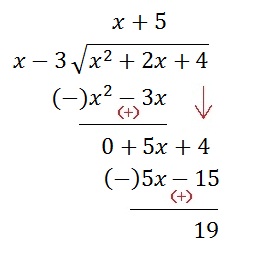
The quotient is the oblique asymptote.
Therefore, the oblique asymptote for the given function is

