Question

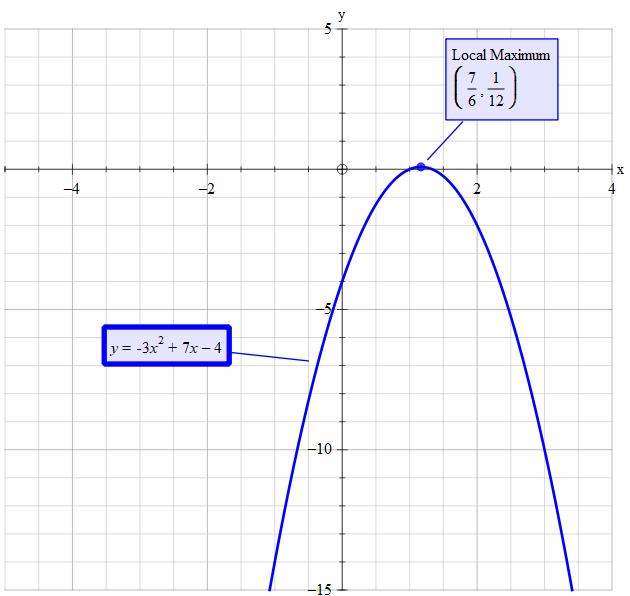
How do you find the axis of symmetry, and the maximum or minimum value of the function `f(x)= -3x^2+7x-4`?

Answer 1

See the explanation: A sort of cheat approach.

Explanation:

Firstly the coefficient of `x^2` is negative so the graph is of form `nnn`. Thus we have a maximum.

Write the equation as: `y=-3(x^2color(red)(-7/3)x)-4`

Thus `x_("maximum")` is at `x=(-1/2)xx(color(red)(-7/3))=+7/6`

Now it is just a matter of substitution to determine `y_("maximum")`