Question

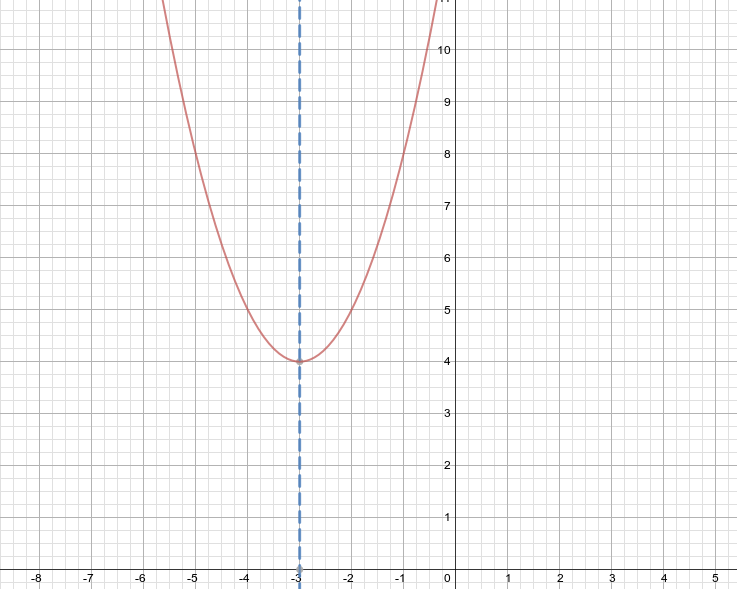
How do you find the axis of symmetry for a quadratic equation `y = x^2 + 6x + 13`?

Answer 1

The axis of symmetry of a quadratic equation is the line parralel to the `Oy` axis passing through the vertex of the parabola. Therefore, we need the `x_v` coordinate of the vertex. `V(x_v, y_v)`

For a quadratic equation `f(x)=ax^2 + bx +c`, we have the following formulae for the coordinates of the vertex:
`x_v=-b/(2a)` and `y_v= -Delta/(4a)`, where `Delta = b^2-4ac`

Therefore, `x_v= -6/(2*1)=-3`

So, the axis of symmetry of the equation `y=x^2+6x+13` is the line defined by the equation `x=-3`.