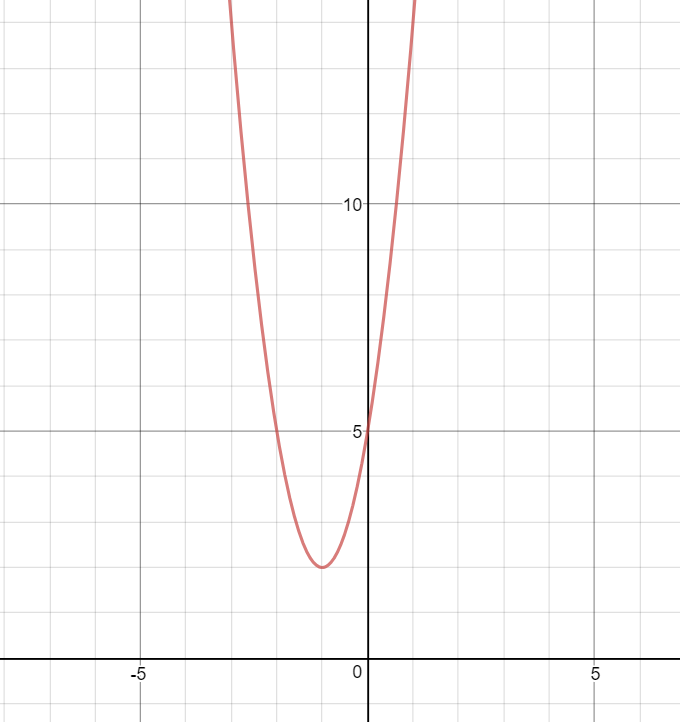
How do you find the axis of symmetry, graph and find the maximum or minimum value of the function #y = 3x^2 + 6x + 5#?
1 Answer
Axis of symmetry:
Maximum or minimum?: minimum
For graph, refer to explanation.
Explanation:
Axis of symmetry means the line that makes the graph symmetrical.
This equation is written in standard form, or
We know that
We write the axis of symmetry as a line, so
The maximum/minimum of a quadratic equation is also the vertex, since it is the highest or lowest point of the parabola.
To find the vertex, we need to do a couple things:
We have already found the axis of symmetry, which was
Now, we need to find the y-coordinate of the vertex, and to do so, we plug back our value of x back into the equation and solve:
So our vertex is
To find whether it is a maximum or minimum, we look at the coefficient. The coefficient here is
When the coefficient is positive (like in this case), then the vertex is the minimum.
When the coefficient is negative, then the vertex is the maximum.
Here is the graph of our equation