Question

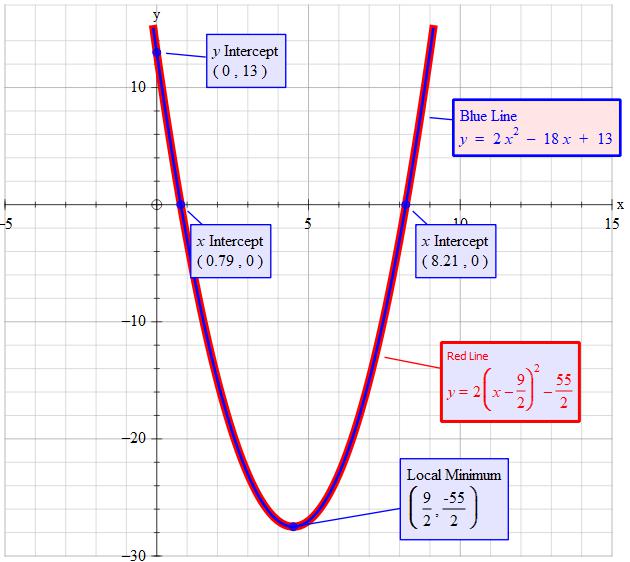
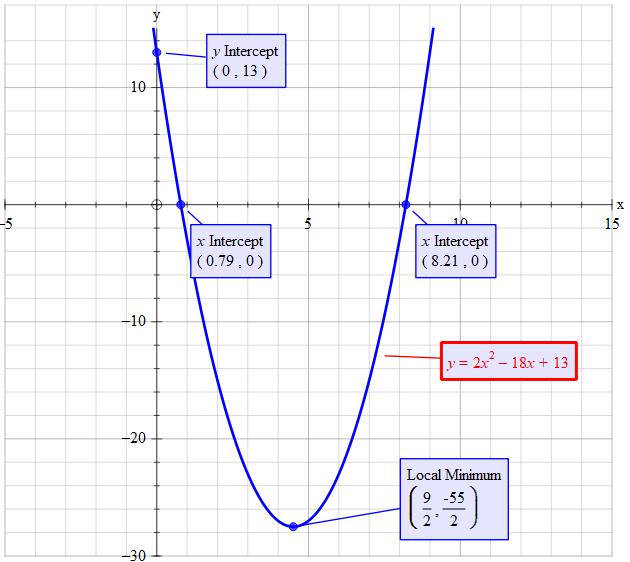
How do you find the axis of symmetry, graph and find the maximum or minimum value of the function `y=2x^2 - 18x +13`?

Answer 1

Axis of symmetry: `x=9/2`

Vertex (minimum point): `(9/2,-55/2)`

X-intercepts: `((9+sqrt55)/2,0)` and `((9-sqrt55)/2,0)`

Y-intercept: `(0,13)`

Refer to the explanation for the process and approximate values for vertex, x-intercepts, and y-intercept.

Explanation:

Given:

`y=2x^2-18x+13` is a quadratic equation in standard form:

`y=ax^2+bx+c`,

where:

`a=2`, `b=-18`, and `c=13`

To graph a quadratic function, you need to have at least the vertex and x-intercepts. The y-intercept is helpful, also.

Axis of Symmetry: vertical line `(x,+-oo)` that divides the parabola into two equal halves. The variable for the line is `x=(-b)/(2a)`.

`x=(-(-18))/(2*2)`

`x=18/4`

`x=9/2` `larr` axis of symmetry and `x`-value for the vertex

Vertex: the maximum or minimum point of the parabola. If `a>0`, the vertex is the minimum point and the parabola will open upward. If `a<0`, the vertex is the maximum point and the parabola will open downward.

We have the `x`-value of the vertex. To determine the `y`-value, substitute `9/2` for `x` in the equation and solve for `y`.

`y=2(9/2)^2-18(9/2)+13`

Simplify.

`y=2(81/4)-162/2+13`

All terms must have a common denominator of `4`. Multiply fractions without a denominator of `4` by a multiplier equal to `1` that will produce an equivalent fraction with a denominator of `4`. For example, `color(magenta)3/color(magenta)3=1` Recall that any whole number, `n`, is understood to have a denominator of `1`. So `13=13/1`

`y=162/4-162/2xxcolor(red)2/color(red)2+13/1xxcolor(blue)4/color(blue)4`

`y=162/4-324/4+52/4`

`y=((162-324+52))/4`

`y=(-110)/4`

`y=-55/2`

Vertex: `(9/2,-55/2)` `larr` minimum point of the parabola

Approximate vertex: `(4.5,-27.5)`

Substitute `0` for `y` and use the quadratic formula to find the roots and the x-intercepts.

`0=2x^2-18x+13`

`x=(-b+-sqrt(b^2-4ac))/(2a)`

Plug in the known values.

`x=(-(-18)+-sqrt((-18)^2-4*2*13))/(2*2)`

Simplify.

`x=(18+-sqrt(324-104))/4`

`x=(18+-sqrt(220))/4`

Prime factorize `220`.

`x=(18+-sqrt((2xx2)xx5xx11))/4`

`x=(18+-2sqrt(55))/4`

Simplify.

`x=(9+-sqrt55)/2`

Roots: values for `x`

`x=(9+sqrt55)/2`,`(9-sqrt55)/2`

Approximate values for `x`.

`x=8.21,` `0.792`

X-intercepts: values of `x` when `y=0`

`x`-intercepts: `((9+sqrt55)/2,0)` and `((9-sqrt55)/2,0)`

Approximate `x`-intercepts: `(8.21,0)` and `(0.792,0)`

Y-Intercept: value of `y` when `x=0`

`y=2(0)^2-18(0)+13`

`y=13`

Y-intercept: `(0,13)`

Plot the vertex and x-intercepts and sketch a parabola through the points. Do not connect the dots.

graph{y=2x^2-18x+13 [-13.95, 18.07, -40.31, -24.29]}

Answer 2

Some notes on Quadratic equation plots

Explanation:

`color(blue)("Axis of symmetry - a sort of cheat method")`

This uses the beginnings of completing the square.

Write as: `y=2(x^2-18/2x)+13`

`color(red)(x_("vertex")=x_("axis of symmetry")=)(-1/2)xx(-18/2) = color(red)(+ 4.5 -> 9/2)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("y-intercept")`
This takes on the value of `c` in `y=ax^2+bx+c`

`color(red)(y_("intercept")=c=+13 ->(x,y)=(0,13)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("x-intercepts and vertex")`

Note that the vertex is the point of maximum or minimum.

2 of these x-intercepts exist if the graph crosses the x-axis

1 of these exists if the x-axis is tangential to the vertex.
Some people state that there is still two but they are the same as each other.

Sometimes determining these can take a bit or work. Other times not so.

Initial step is to set `y=0` It has to be 0 for the graph to cross the axis as x-axis is at `y=0`

`y=0=2x^2-18x+13`

If you can spot how to factorise this then that would be the quicker method. For most people this only works if the factors are whole numbers. In this case they are not whole numbers.

There are two options: completing the square or using the other formula.

`y=ax^2+bx+c` where `a=2; b=-18; c=13`

`x_("intercept")=(-b+-sqrt(b^2-4ac))/(2a)" ".......Equation color(white)("d")type1`

`y=0=a(x+b/(2a))^2+k+c" ".......Equation color(white)("d")type2`

`Equation color(white)("d") type 2` can be used to directly determine both the vertex and x-intercepts.

Part of `Equation color(white)("d")type1` can be used to indicate if the plot actually has an x-intercept.

The determinant `->b^2-4ac` must be such that `b^2-4ac>=0`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The original equation and the completed square are different forms of the same condition. As such the plot of one will be the same as the plot of the other.

Zoom in and you will see that the blue plot follows the same path as the red.