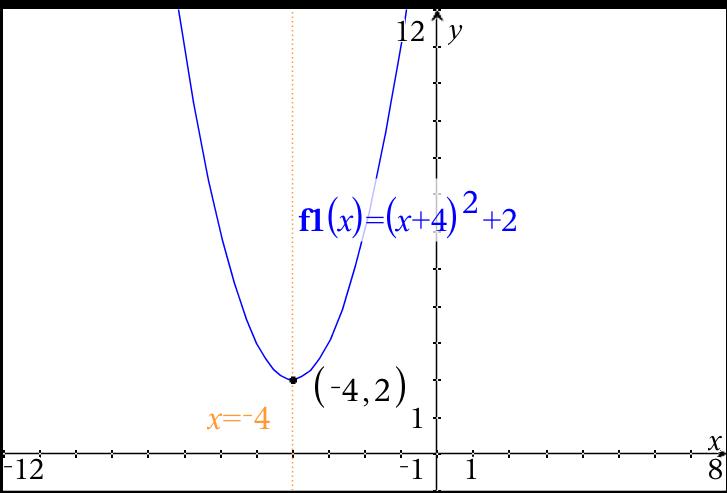
How do you find the axis of symmetry, graph and find the maximum or minimum value of the function #y=(x+4)^2+2#?
1 Answer
Jan 31, 2017
The vertex form for a quadratic looks like:
Explanation:
The axis of symmetry must go through the vertex, so it is the line
Since the leading coefficient, or multiplier on
Here is the graph: