Question

How do you find the axis of symmetry, vertex and x intercepts for `y=2x^2+4x-1`?

Answer 1

Axis of Symmetry : `color(red)(x=(-1))`

Vertex : `color(red)((-1,-3)`

x-intercepts : `color(red)((0.223,0) and (-2.225,0)`

Explanation:

`" "`
We are given the quadratic function

`color(blue)(y=f(x)=2x^2+4x-1`

The general form of the quadratic function is

`color(red)(y=f(x)=ax^2+bx+c`

We have,

`(a=+2); (b=+4) and (c=-1)`

Set

`color(blue)(y = f(x)=0`

`:. color(red)(y=f(x)=2x^2+4x-1=0`

This is our quadratic equation.

To find the Vertex, use the formula `color(red)(((-b)/(2a))`

`rArr (-4)/(2(2)`

`rArr -4/4`

`rArr -1`

This is the x-coordinate value of the Vertex.

To find the y-coordinate value of the Vertex,

substitute this value of `color(green)(x=-1)`

Set `color(red)((x=-1)`

Hence, `color(blue)(y=2(-1)^2+4(-1)-1`

`rArr 2-4-1`

`rArr (-5)+2`

`rArr (-3)`

Hence, the Vertex is `color(red)((-1, -3)`

Set `color(blue)(y=0)` to find the x-intercepts

`rArr 2x^2+4x-1=0`

This is a quadratic equation - a polynomial of degree 2

Use the quadratic formula to find the solutions.

`color(blue)(x_1, x_2 = [-b+- sqrt(b^2-4ac)]/(2a)`

Use the values:

`(a=+2); (b=+4) and (c=-1)`

`color(blue)(x_1, x_2 = [-4+- sqrt(4^2-4(2)(-1))]/(2(2))`

`rArr [-4+- sqrt(16+8)]/(4)`

`rArr [-4+- sqrt(24)]/(4)`

`rArr [-4+- sqrt(4*6)]/(4)`

`rArr [-4+- sqrt(4)*sqrt(6)]/(4)`

`rArr [-4+- 2*sqrt(6)]/(4)`

`x_1, x_2= [[-4+ 2*sqrt(6)]/(4)], [[-4- 2*sqrt(6)]/(4)]`

`x_1, x_2~~ [0.224744871],[-2.224744871]`

`color(blue)(x_1, x_2~~ [0.223],[-2.225]`

These are our x-intercepts.

Axis of Symmetry is the x-coordinate value of the Vertex.

Hence,

Axis of Symmetry : `color(red)(x=(-1))`

Vertex : `color(red)((-1,-3)`

x-intercepts : `color(red)((0.223,0) and (-2.225,0)`

Please examine the graph below for a visual comprehension:

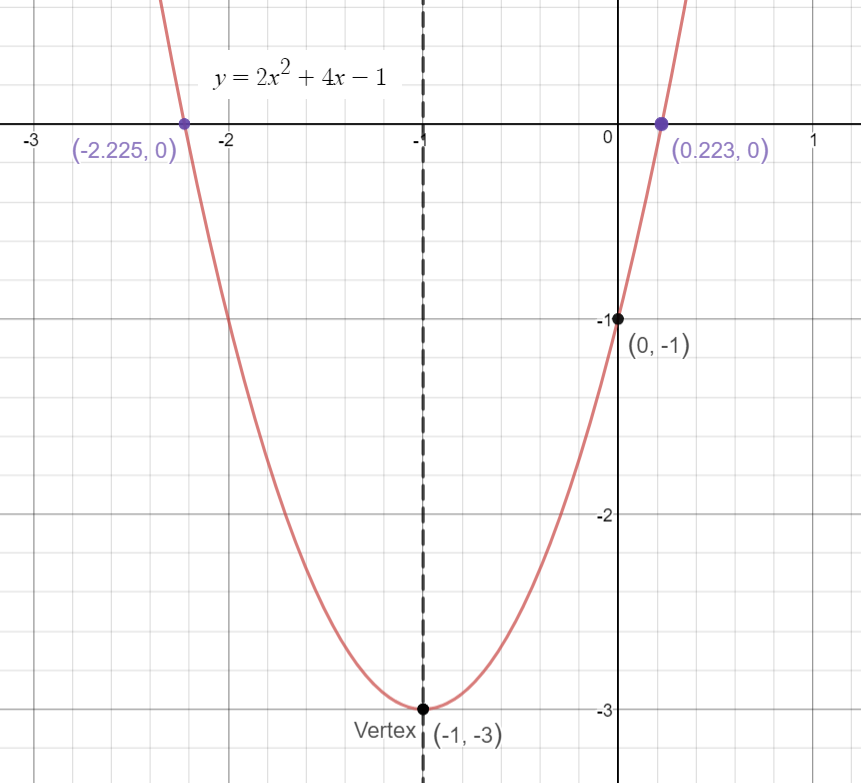
Hope it helps.