How do you find the binomial expansion of #(x + y)^7#?
1 Answer
Aug 31, 2015
Use the Binomial Theorem and Pascal's triangle to find:
Explanation:
The Binomial Theorem tells us:
where
So in our case:
These
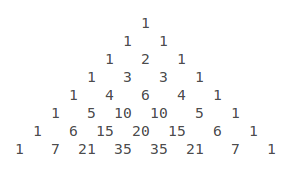
Each number is formed by adding the two numbers above to the left and right.
The last row gives us the coefficients we need:

