How do you find the center of mass if the density at any point is inversely proportional to its distance from the origin of a lamina that occupies the region inside the circle #x^2 + y^2 = 10y# but outside the circle #x^2+y^2=25#?

1 Answer
Steve M
Jan 10, 2017

The enter of mass is #(0, 2.5)#

Explanation:

Consider the first equation:

# x^2+y^2=10y #

We can put this into standard from by completing the square:

# x^2 + y^2 - 10y = 0 #
# :. x^2 + (y-5)^2-5^2 = 0 #
# :. x^2 + (y-5)^2 = 5^2 #

Which is a circle of radius #5# and centre #(0,5)#, And now the second equation:

# x^2+y^2=25 #

Which is a circle of radius #5# and centre #(0,0)#

We can plot these curves;
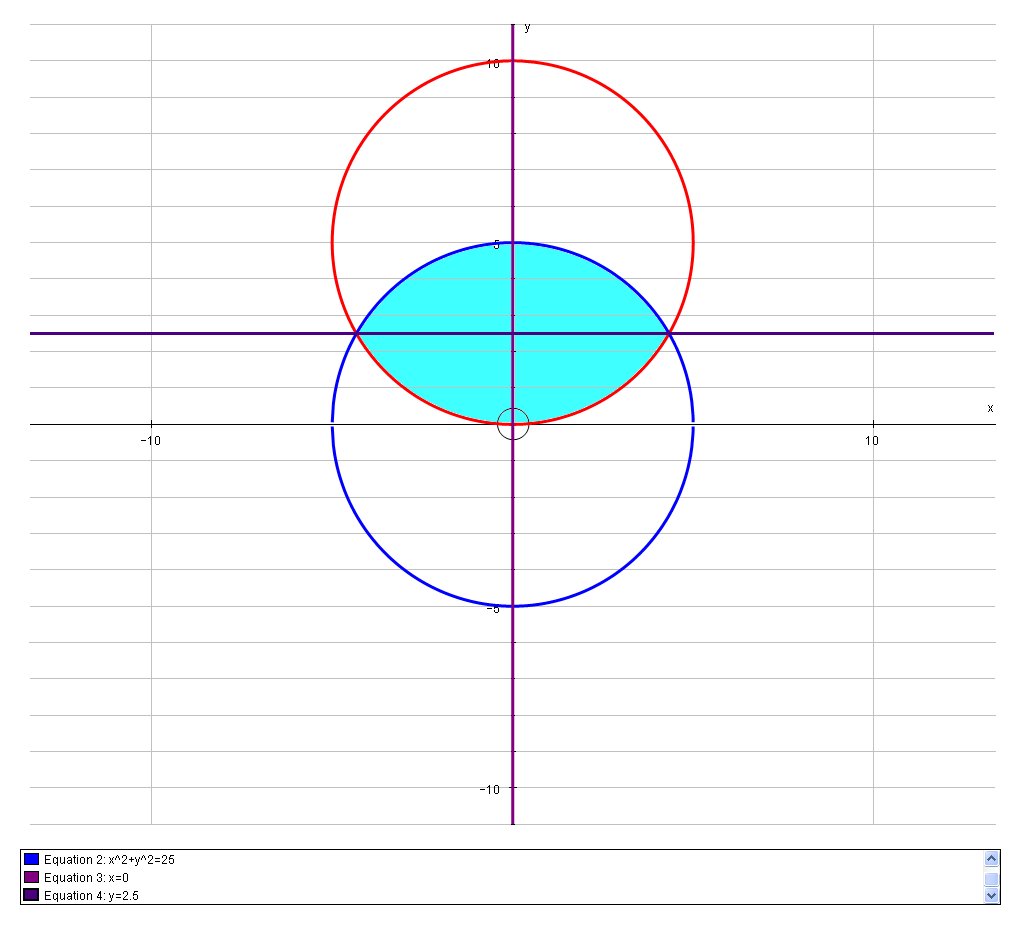
enter image source here

For a more complex problem we would need to use integration to find the Centre of Mass, but because of symmetry the density will be evenly distributed about the lines #x=0# and #y=2.5#, these being the lines of symmetry.

Hence the enter of mass is #(0, 2.5)#

Related questions
See all questions in Calculating Areas using Integrals
Impact of this question
10254 views around the world
You can reuse this answer
Creative Commons License