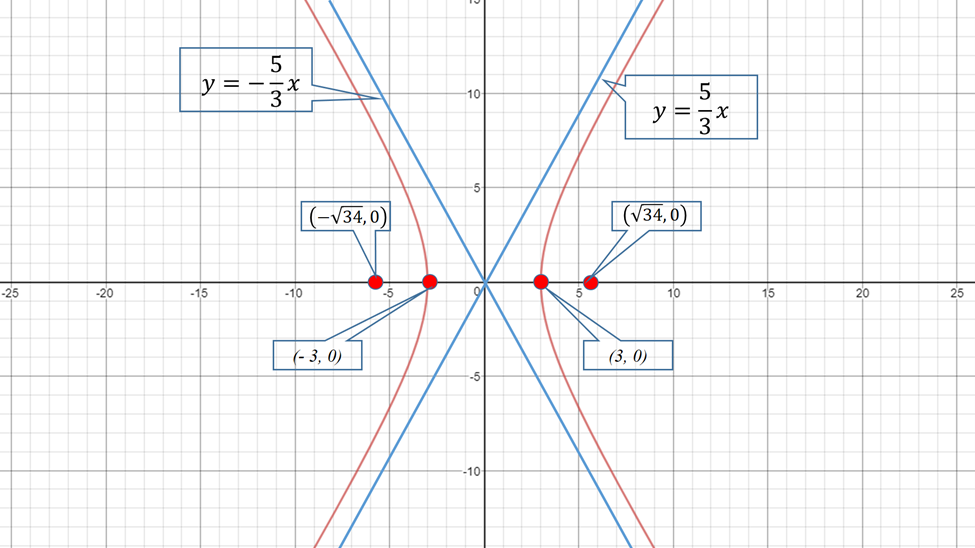
How do you find the coordinates of the vertices, foci, and the equation of the asymptotes for the hyperbola #x^2/9-y^2/25=1#?

Question

2703 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-26T02:12:23

vertices #(3,0) and (-3.0)#
Foci #(sqrt34,0) and (-sqrt34, 0)#
Aymptotes #y=5/3 x and y= - 5/3 x#

Given -

#x^2/9-y^2/25=1#

This hyperbola equation is in the form

#x^2/a^2-y^2/b^2=1#

If this is the case then

Its vertices are #(a, 0) and (-a,0)#
Its foci are #(c,0) and (-c,0)#

Its asymptotes are #y=b/a x and y = - b/a x#

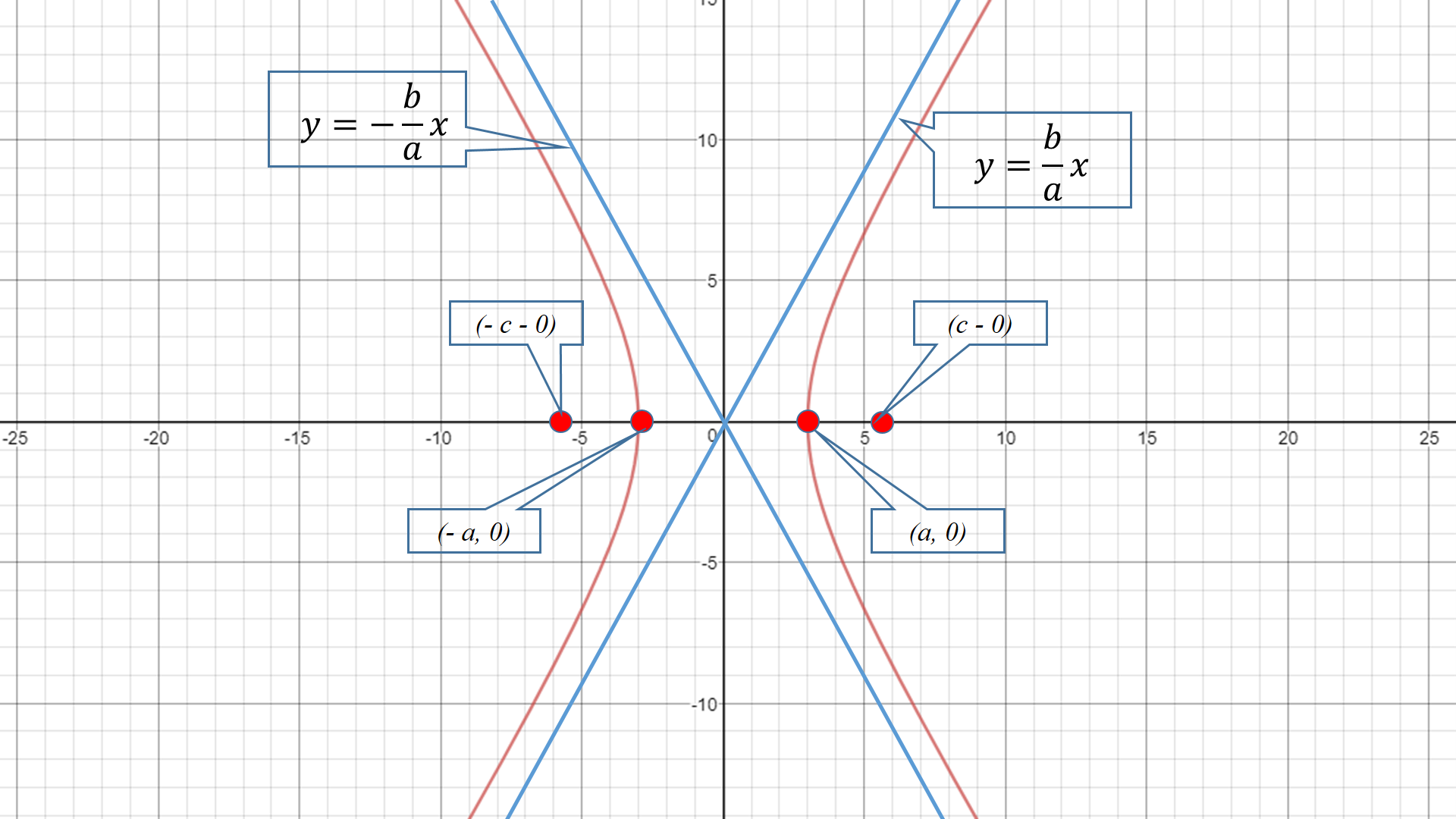
enter image source here

Then we have to find the values of #a,b and c # from the given equation.

#a=sqrt(9)=3#
#b=sqrt25=5#
#c^2=a^2+b^2#
#c=+-sqrt (9+25)=+-sqrt34#

Then
vertices #(3,0) and (-3.0)#
Foci #(sqrt34,0) and (-sqrt34, 0)#
Aymptotes #y=5/3 x and y= - 5/3 x#

enter image source here