How do you find the distance between #(2, π/3), (5, 2π/3)#?
2 Answers
The distance is
Explanation:
We convert the polar coordinates
and
The distance is between
Here is a graph of vectors from the origin to the two points:
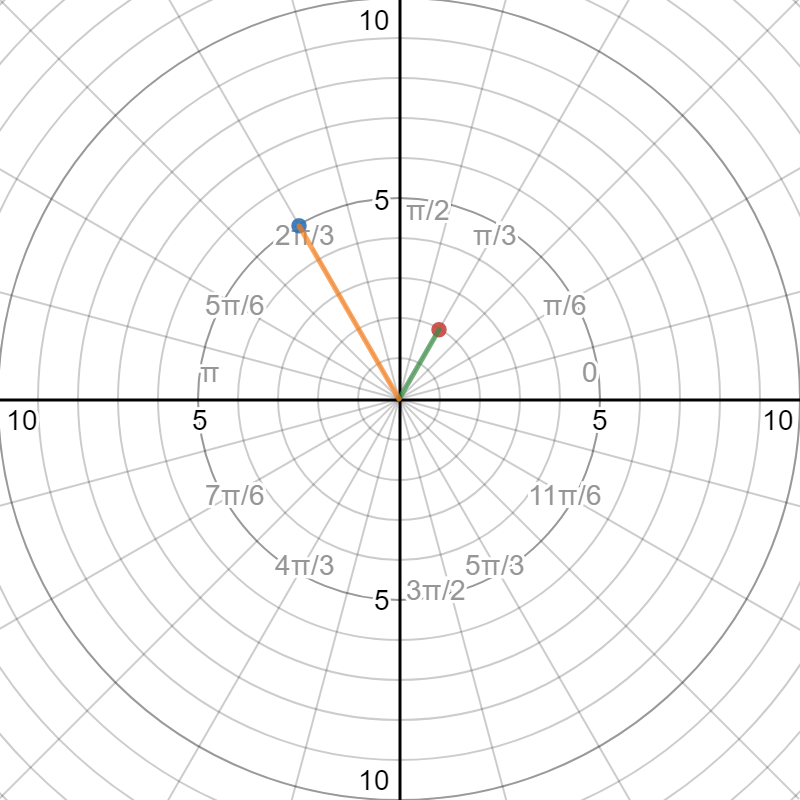
Explanation:
Please observe that the line connecting the two points forms a triangle:
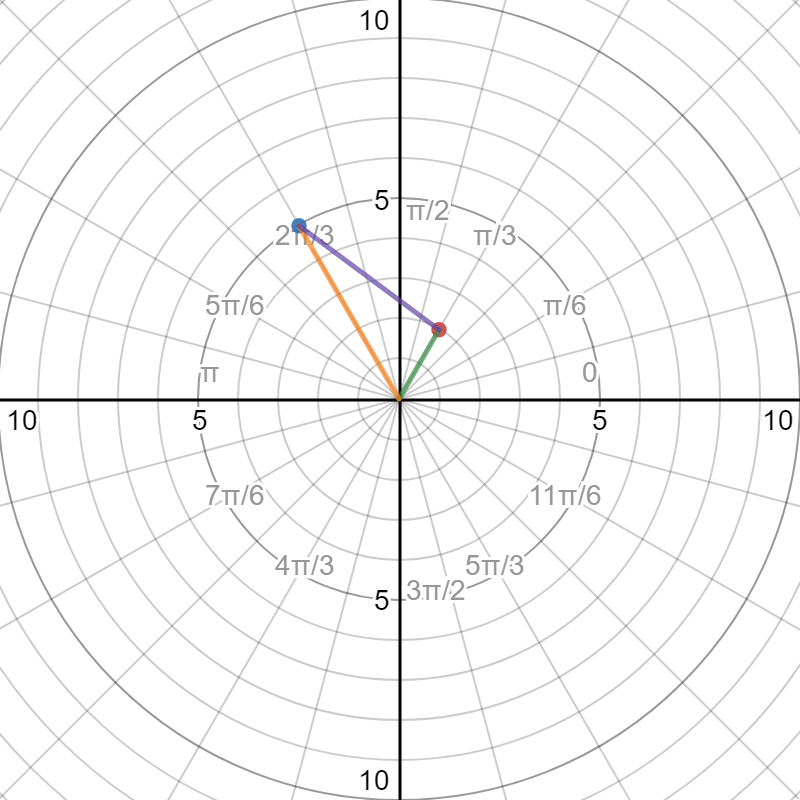
We can use the Law of Cosines to find the length of the blue line (side c):
Where

