How do you find the distance between (20,-10), (8,6)?
3 Answers
Explanation:
Distance,
Let say
therefore,
Explanation:
First off, the distance formula should be known
#d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#
Simply substitute
#d=sqrt((8-20)^2+(6-(-10)^2)#
Now solve
#d=sqrt((8-20)^2+(6+10)^2)#
#d=sqrt((-12)^2+16^2)#
#d=sqrt(144+256)#
#d=sqrt400#
#d=20#
20
Explanation:
Here's a graph of the situation, where the dots are the given points.
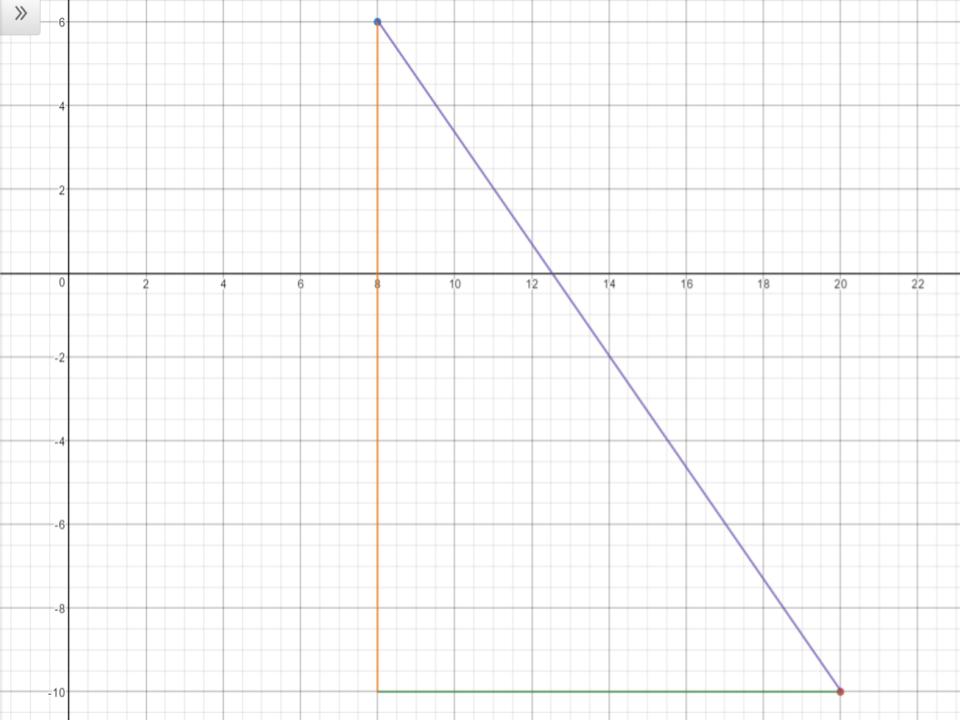
We're trying to calculate the length of the purple line (hypotenuse) here. We can find the length of the green and yellow lines as follows:
GREEN (bottom line):
YELLOW (vertical line):
Then we can use the Pythagorean theorem to find the length of the purple line (P):
So the distance between the points is 20 units.
In general in 2D Euclidean space (or the x-y plane if that's how you know it),
Length



