How do you find the domain and range of # (2/3)^x – 9#?
1 Answer
Jul 31, 2016
Domain:
Range:
Explanation:
For the domain:
x can take any value. Therefore
Domain:
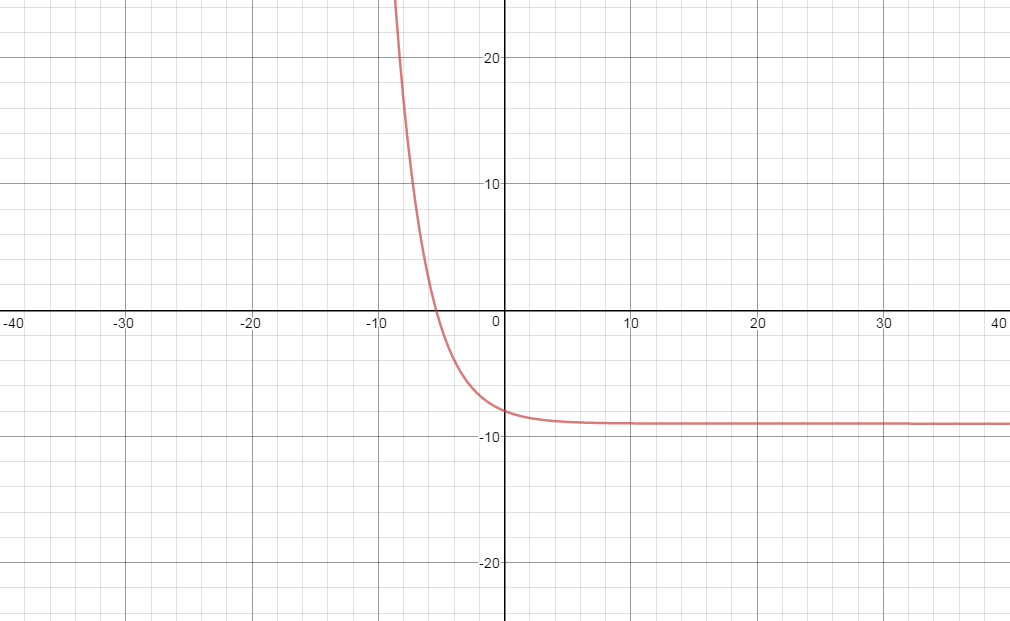
The horizontal asymptote of the graph is
Range:
Kindly see the graph for visual aid.
God bless....I hope the explanation is useful.
