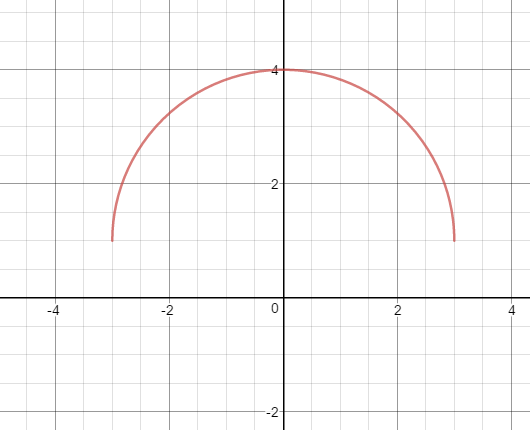
How do you find the domain and range of #f(x) = 1 + sqrt(9 - x^2)#?

Question

4942 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-05T23:30:58

The domain of #f(x)# is all the values for which

#9-x^2>=0#

#(3-x)*(3+x)>=0#

Which is valid for #x# in #[-3,3]#

Hence the domain is #D_f=[-3,3]#

For the range of the function we have that

#f(-3)=f(3)=1#

and the maximum value of f(x) is achieved when

#9-x^2# is maximized which happens for #x=0#

and that is #f(0)=4#

Hence the range of the function is

#R_f=[1,4]#

The graph of the function is

enter image source here