Question

How do you find the domain and range of `f(x) = (2x)/(sqrt(16-8x))`?

Answer 1

Domain:

The domain will be determined by saying that the radical has to be larger than `0`, this being because it's a rational function as well as a radical function.

Consider the function `y = 1/x`.

The domain would be `x !=0`, since if x was equal to 0, then the function would be non-defined.

Now consider the function `y = 1/sqrt(x)`.

Recall that a square root is undefined in the real number system if the number inside the square (the radicand) is less than 0 (`x < 0`). At this point, the domain is `x >= 0`. However, since the radical is in the denominator, and the denominator cannot be equal to `0`, the domain is made `x > 0`, or the `0` is excluded.

Back to our function at hand:

`sqrt(16 - 8x) > 0`

`16 - 8x > 0`

`16 > 8x`

`2 > x`

Hence, the domain is `x< 2,`

The graph of the function, shown in the following image, justifies our answer.

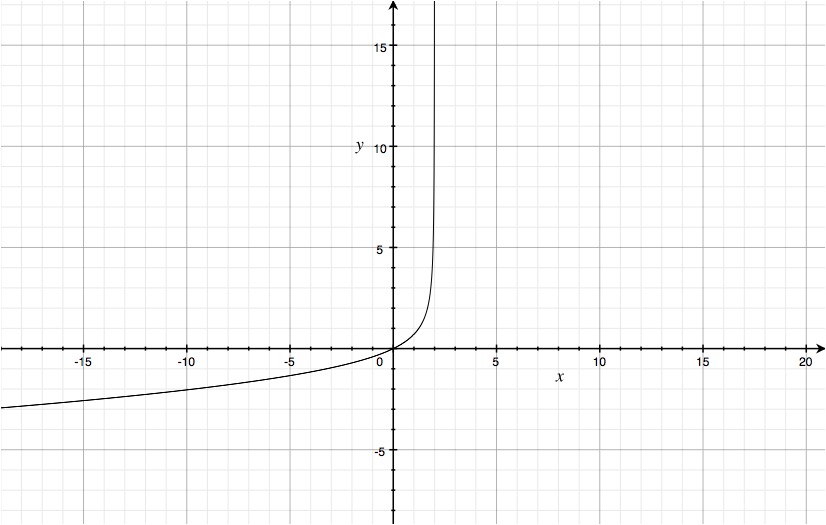
Range:

From as far as I can tell, the range is all the real numbers. I looked at the graph to huge numbers (ex. `2.08 xx 10^4)`, and it looked like the y values were continuing to reduce to `-oo`, indicating the presence of no horizontal asymptotes.

Thus, the range is `y in RR`.

In summary:

For the function `f(x) = (2x)/sqrt(16 - 8x)`:

•The domain is `x < 2`

•The range is `y in RR`

Practice Exercises:

Determine the domain and range of the function `g(x) = (4x)/sqrt(2x^2 + 11x + 12)`.

Hopefully this helps, and good luck!