How do you find the domain and range of #f(x) = (x + 5)^2 + 8#?
1 Answer
Domain:
Using Interval Notation:
Range:
Using Interval Notation:
Explanation:
Given:
The Vertex Form of a quadratic function is:
Note:
Vertex is at :
Note :
If
Since,
Using Interval Notation :
Find Domain :
Domain of
The function does not have any domain constraints.
Therefore domain is given by
Using Interval Notation :
Hence, the required solutions are:
Domain:
Using Interval Notation:
Range:
Using Interval Notation:
Draw the graph of
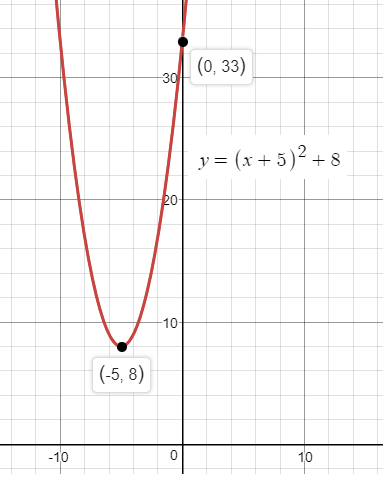
Hope it helps.

