Start by thinking of the graph for y=log_5 x. If you wrote this in exponential form, it would look like this: 5^y=x.
Go ahead and graph log_5x on your calculator or on Desmos.com so you can reference it.
The x-intercept of a function is where y=0. We know that 5^0=1.
Therefore, you have a point on that graph at (1,0). This is true for all graphs where n is a number and you have y=log_nx.
You also have an asymptote at x=0 because there's no way to make 5^n<=0.
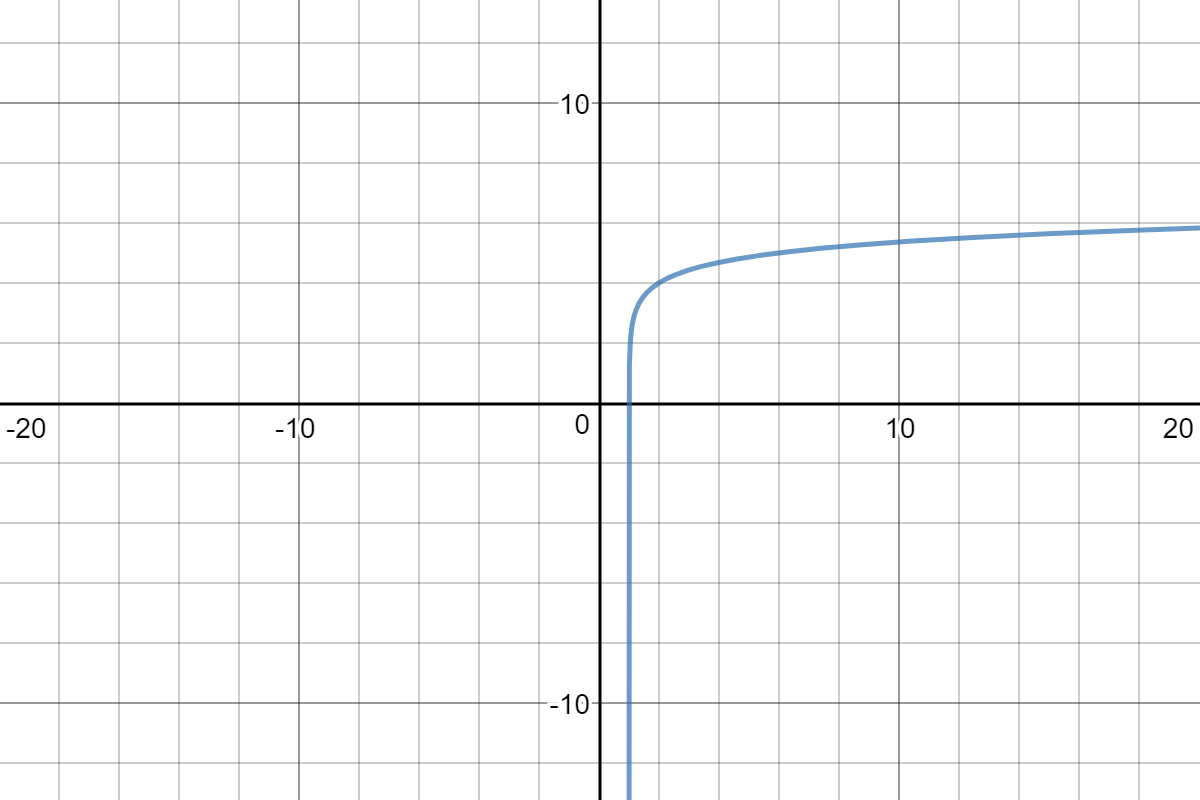
Back to the transformed function: We know that y=log_5 (x-1) is the same as y=log_5 x moved one unit to the right. (If you don't know this, go back and review your transformations of functions rules.)
This puts our new x-intercept at (2,0) instead of (1,0).
The new vertical asymptote is at x=1.
The +4 there at the end moves the graph up four units, which moves that point from (2,0) to (2,4). The asymptote doesn't change, since this is strictly a vertical shift.
Finally, to find the new x-intercept, set y=0 and solve for x:
0=log_5(x-1)+4
Subtract 4 from both sides:
-4=log_5(x-1)
Rewrite the function in exponential form: 5^(-4)=x-1
Use your calculator to figure out 5^(-4)=1/625=1.0016
Add 1 to both sides: 1/625+1=x
Simplify the left side to get 2.0016=626/625=x where the graph intercepts the x-axis. It's okay to use either the decimal or the fraction here since the decimal terminates after four places.
Finally, once you get this, pat yourself on the back! Great job! (But if you still have questions, come back and ask.)