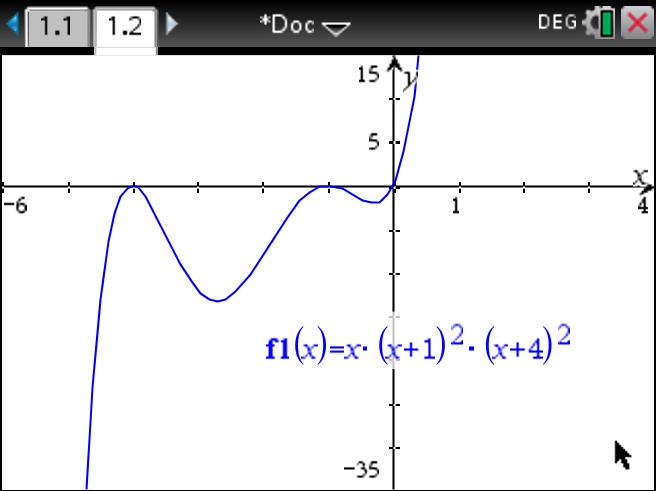
How do you find the end behavior and state the possible number of x intercepts and the value of the y intercept given #y=x(x+1)^2(x+4)^2#?
1 Answer
Dec 8, 2016
End behavior will follow the "parent graph" y =
Explanation:
If you wish to write the end behavior in formal notation, it would look like: 
The x-intercepts would be 0, -1, and -4 by the Zero Product Property.
The graph would cross at 0, and be tangent (or touch and turn around) at -1 and -4 since the factors appear an even number of times.
The y-intercept is found by evaluating at x = 0: y =
(The origin is both the x- and y-intercepts)
Here is the graph: