How do you find the equation, in point slope form, of the line that is perpendicular to the line y=2x-3and passes through the point (1, 2)?

Question

5669 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-16T04:59:29

#color(orange)(x + 2y = 5, " is the standard form of the equation"#

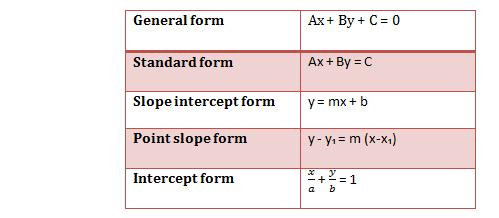
Point Slope Form of equation is #y-y_1 = m * (x - x_1)#

Given : #(x_1,y_1) = (1,2)#

#y = 2x - 3#

Above equation is in the form #y = mx + c, where m = 2#

Slope of line perpendicular to #y = 2x - 3 # is # = -1/m = -1/2#

#:. (y - 2) = -(1/2) * (x - 1)#

#2y - 4 = -x + 1#

#color(orange)(x + 2y = 5, " is the standard form of the equation"#