How do you find the equations of the tangents to #5x^2-4y^2=4# at those points where the curve is cut by #5x-2y=4#?
2 Answers
Explanation:
# 5x^2-4y^2=4 # ..... [1]
# 5x - 2y = 4 # ..... [2]
Step 1 - Find the points of intersection
If we rearrange [2] we get
Substitute into [1]:
# 5x^2-4((5x-4)/2)^2=4 #
# :. 5x^2-4(5x-4)^2/4=4 #
# :. 5x^2-(5x-4)^2=4 #
# :. 5x^2-(25x^2-40x+16)=4 #
# :. 5x^2-25x^2+40x-16=4 #
# :. -20x^2+40x-20=0 #
# :. 20x^2-40x+20=0 #
# :. x^2-2x+1=0 #
# :. (x-1)^2=0 #
# :. x=1 #
Using [1]; When
So there is ONE point of intersection at
Step 2 - Differentiate the equation of the curve
# 5x^2-4y^2=4 #
Differentiating implicitly gives:
# 10x-8ydy/dx=0 #
# :. dy/dx = (10x)/(8y) = (5x)/(4y)# ..... [3]
Step 3 - Find the gradient of the tangent at the points of intersections
The gradient of the tangent at any particular point is given by the derivative, so using [3] at
# dy/dx = ( (5)(1) ) / ( (4)(1/2) ) =5/2 #
Step 4 - Find the equation of the tangent
The tangent passes through
Using
# y - 1/2 = 5/2(x-1) #
# :. 2y - 1 = 5(x-1) #
# :. 2y - 1 = 5x-5 #
# :. 5x-2y=4 #
So The line that the curve intersects with is actually also the tangent
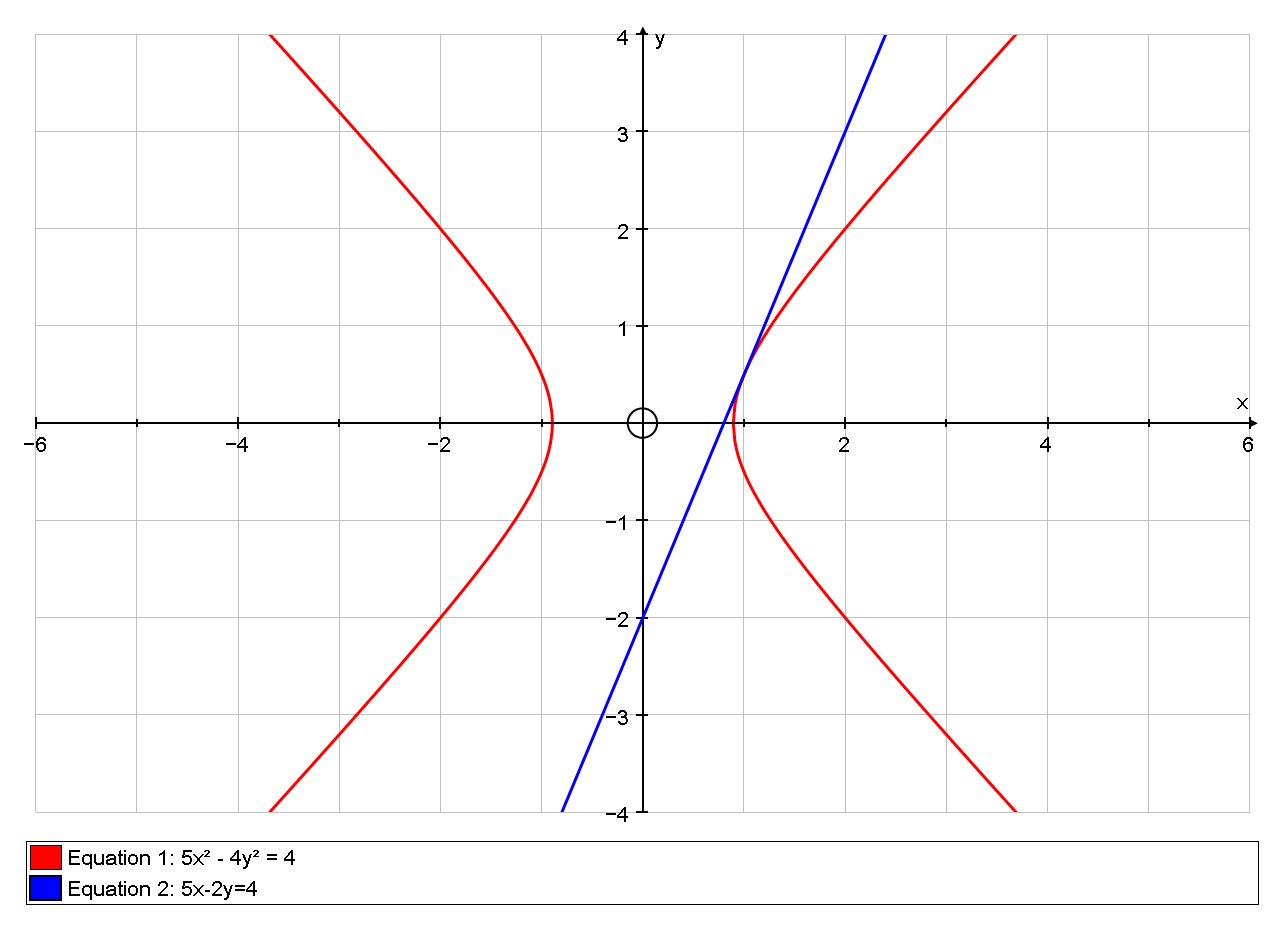
graph{(4y^2-5x^2+4)(5x-2y-4)=0 [-3.96, 4.81, -1.723, 2.66]}
The given line is tangent to the curve in
Explanation:
By the equation of the line
Multiplying the curce equation by 5 and substituting
Simplifying by 4 we get
The solution found comes with multiplicity 2 so the line is tangent to the curve.

