How do you find the exact value of #cos45# using the sum and difference, double angle or half angle formulas?

Question

3052 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-09-30T23:26:31

#cos 45^@ = sqrt(2)/2#

The double angle formula for #cos# can be written:

#cos 2theta = cos^2 theta - sin^2 theta = 2cos^2 theta - 1#

Given:

#cos 90^@ = 0#

Let #theta = 45^@# to get:

#0 = cos 90^@ = 2cos^2 45^@-1#

Add #1# to both ends to get:

#1 = 2cos^2 45^@#

Divide both sides by #2# and transpose to find:

#cos^2 45^@ = 1/2#

Hence:

#cos 45^@ = +-sqrt(1/2) = +-sqrt(2/4) = +-sqrt(2)/2#

Now #45^@# is in Q1, so #cos 45^@ > 0# and we need the positive square root.

So:

#cos 45^@ = sqrt(2)/2#

#color(white)()#
Note

I prefer to find #cos 45^@# by considering a #1:1:sqrt(2)# right angled triangle, formed by cutting a square diagonally in half...

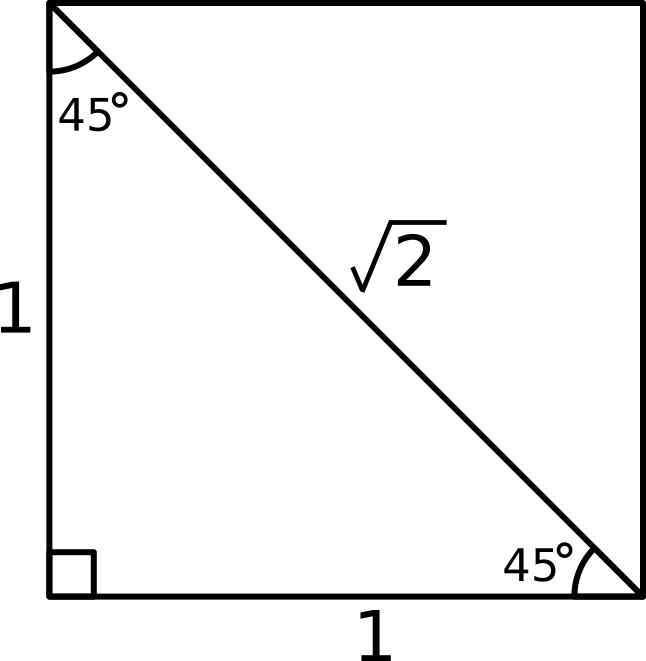
enter image source here

Then:

#cos 45^@ = "adjacent"/"hypotenuse" = 1/sqrt(2) = sqrt(2)/2#