How do you find the exact value of the area in the first quadrant enclosed by graph of y=sinx and y=cosx?
1 Answer
Jan 19, 2017
Explanation:
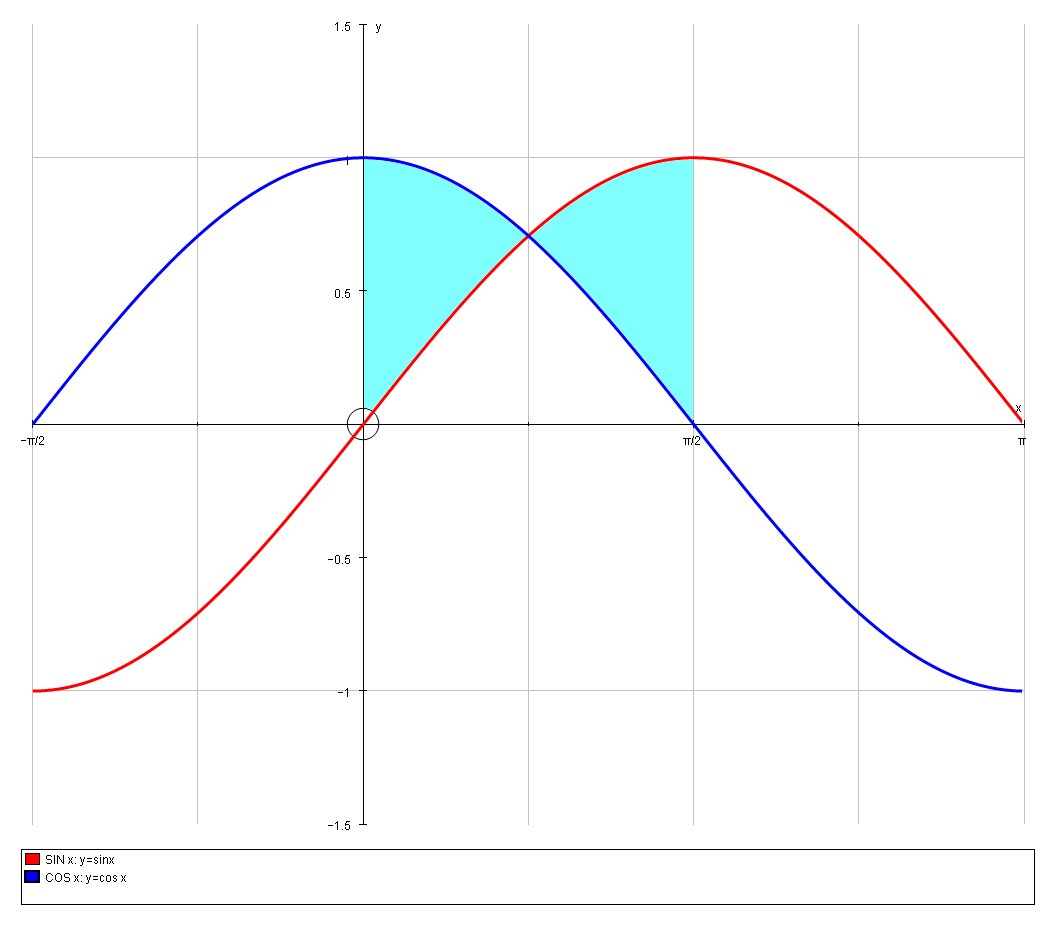
The area enclosed by the graphs
By symmetry this area is
# A= int_0^(pi/4) cosx - sinx \ dx #
# \ \ \ = [sinx +cosx]_0^(pi/4) #
# \ \ \ = { (sin(pi/4)+cos(pi/4)) - (sin 0 + cos 0)} #
# \ \ \ = (1/2sqrt(2)+1/2sqrt(2)) - (0+1)#
# \ \ \ = sqrt(2)-1 #
Hence shaded are is

