Question

How do you find the important parts of the equation to graph the function `y = -x^2 + 3`?

Answer 1

Refer the explanation section

Explanation:

Given -

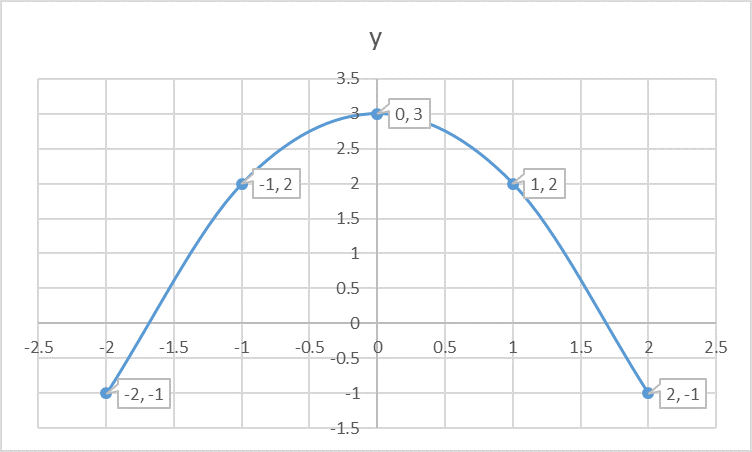
`y=-x^2+3`

Find the vertex first-

If the quadratic equation is in the form `y=ax^2+bx+c`, then it is given by

`x=(-b)/(2a)`

Since there is no `bx` term in the given equation, we shall supply it

`y=-x^2+0x+3`

`x=(-(0))/(2 xx (-1))=0`

At `x=0`

`y=-0^2+3=3`

The vertex is `(0, 3)`

Then we have to decide whether the curve is concave downwards or upwards. That is given by the second derivative.

`dy/d=-2x`
`(d^2y)/(dx^2)=-2<0`

Since the second derivative is less than zero, the curve is concave downwards.

Take two points to the right of zero [ x-coordinate of the vertex] and two points to the left of zero. Find the corresponding `y` value.

Plot the pairs in a graph sheet. Join all the points.

See the Table

See the graph