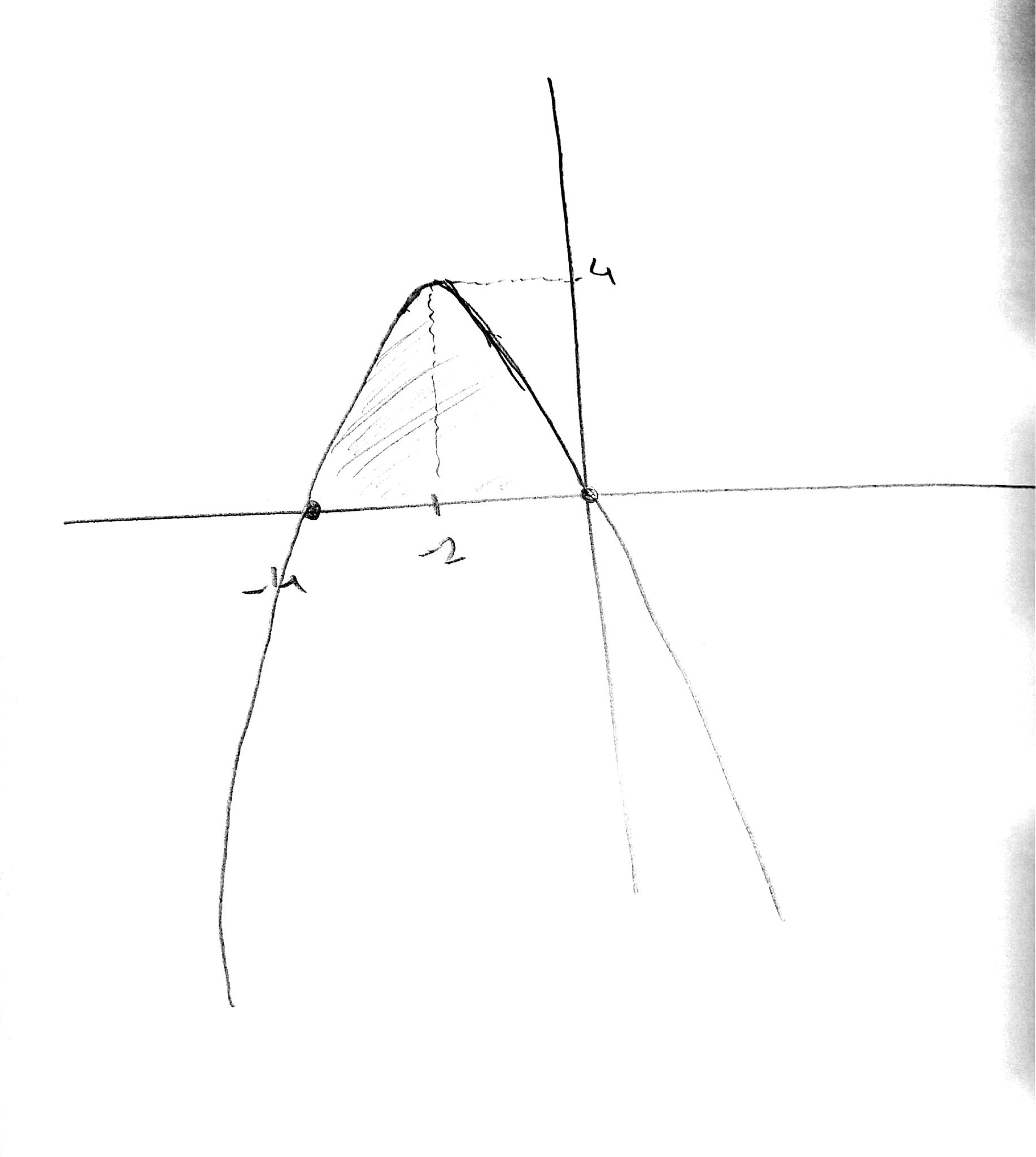
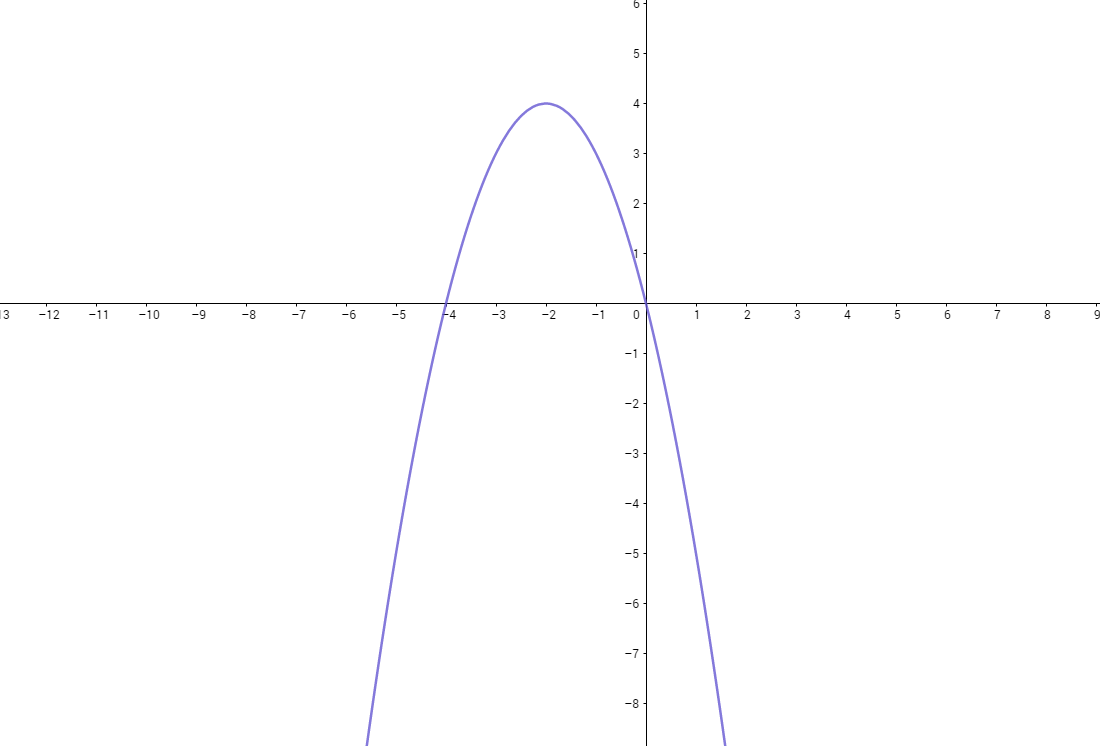
How do you find the important points to graph #f(x)= -x^2-4x#?
1 Answer
Jan 18, 2018
Check below for detail examination of the function.
Explanation:
- We get these tables for monotony and concavity of
#f# :
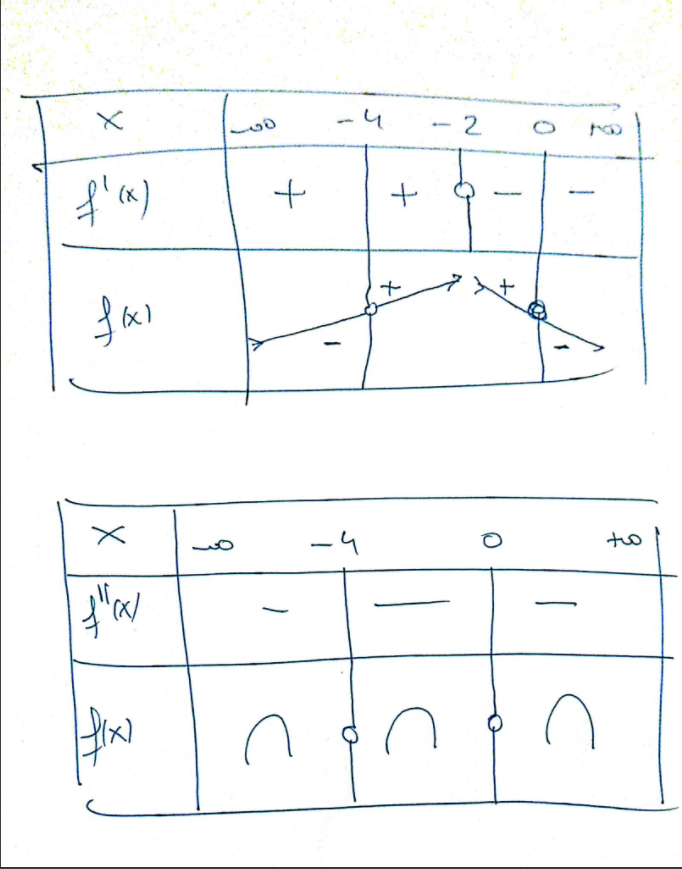
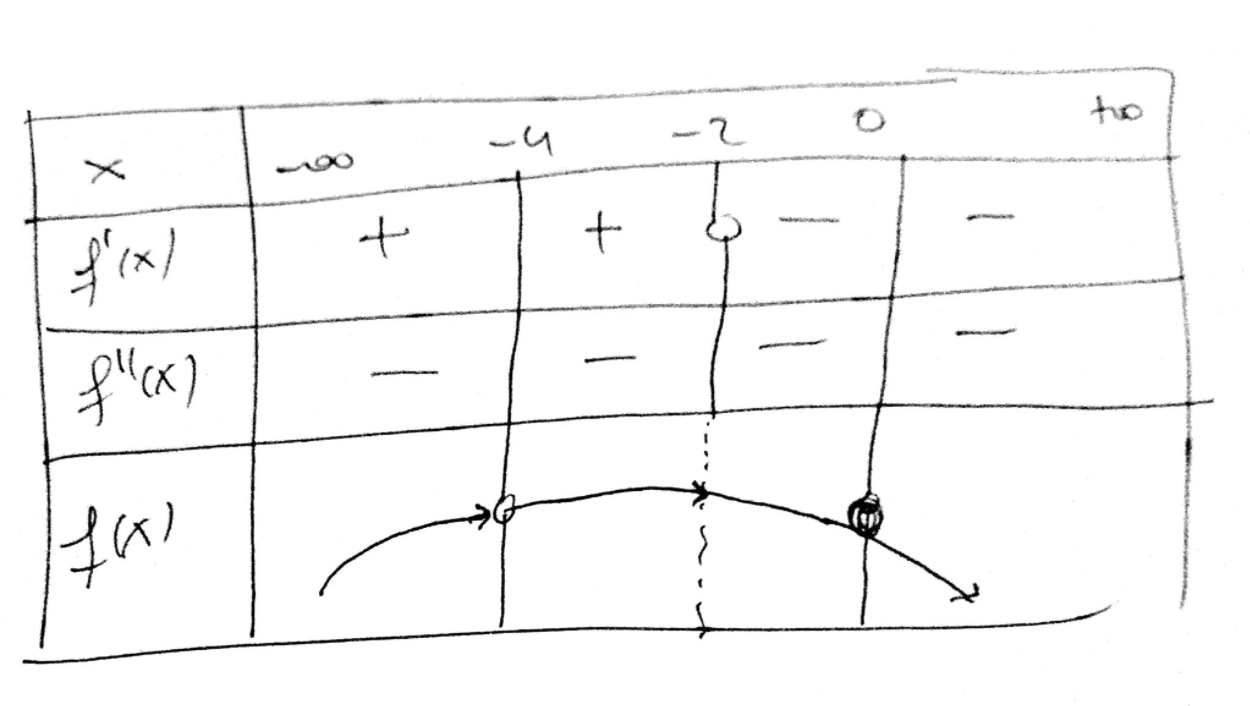
- As a result the range of
#f# will be#(-oo,4]#
- As a result
#f# doesn't have any oblique/horizontal asymptotes.