How do you find the integral of # 3x (sqrt(81-x^2))#?

Question

3680 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-04-20T18:39:04

Have a look:
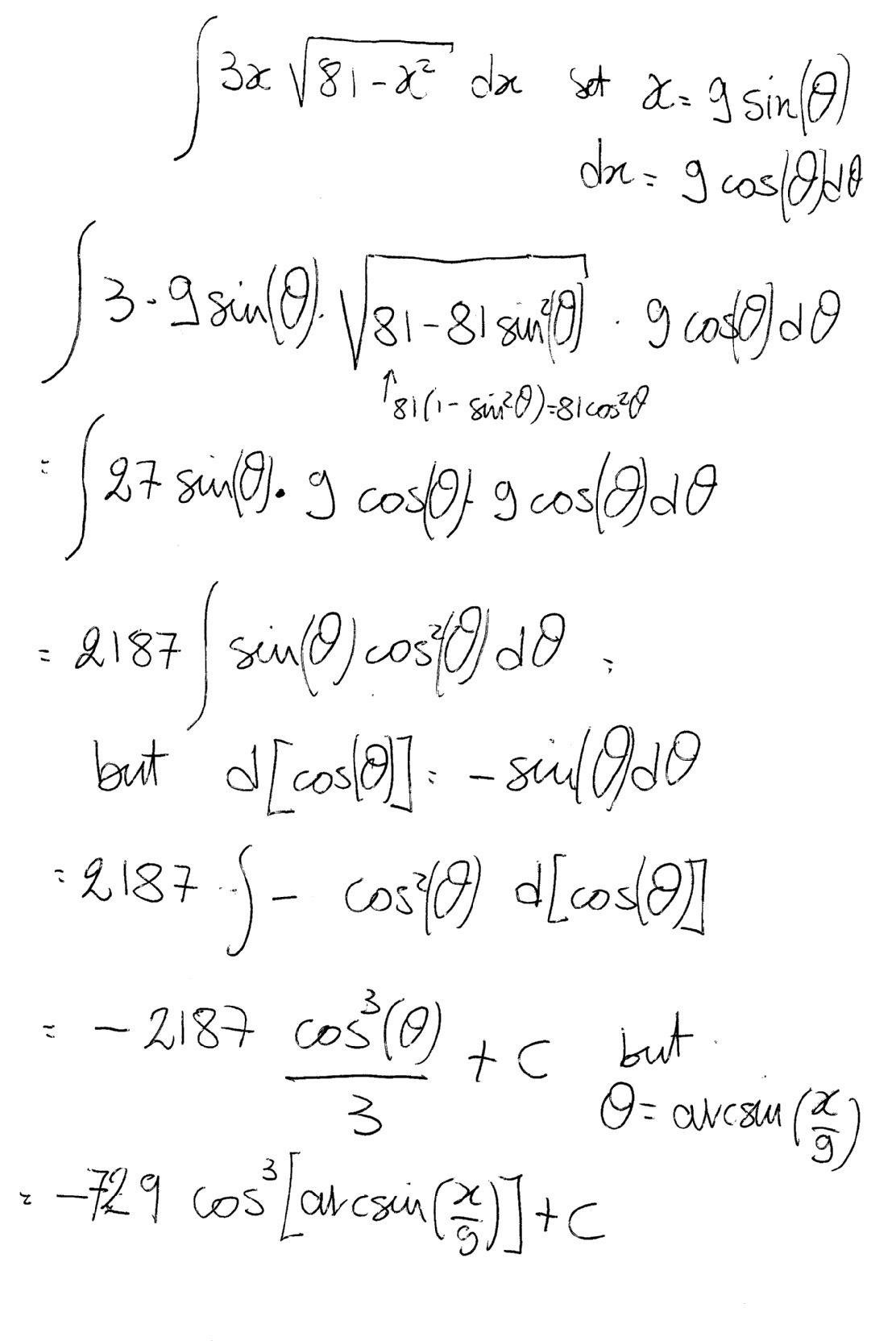
enter image source here

The answer using this method will look like the other, if you use:
#cos(arcsin(x/9)) = sqrt(1- x^2/81)# So

#-729 cos^3(arcsin(x/9)) = -729 (sqrt(1- x^2/81))^3 = -(9sqrt(1- x^2/81))^3 = -(sqrt (81-x^2))^3#

Answer 2 · 2015-04-20T18:39:58

Apr 20, 2015

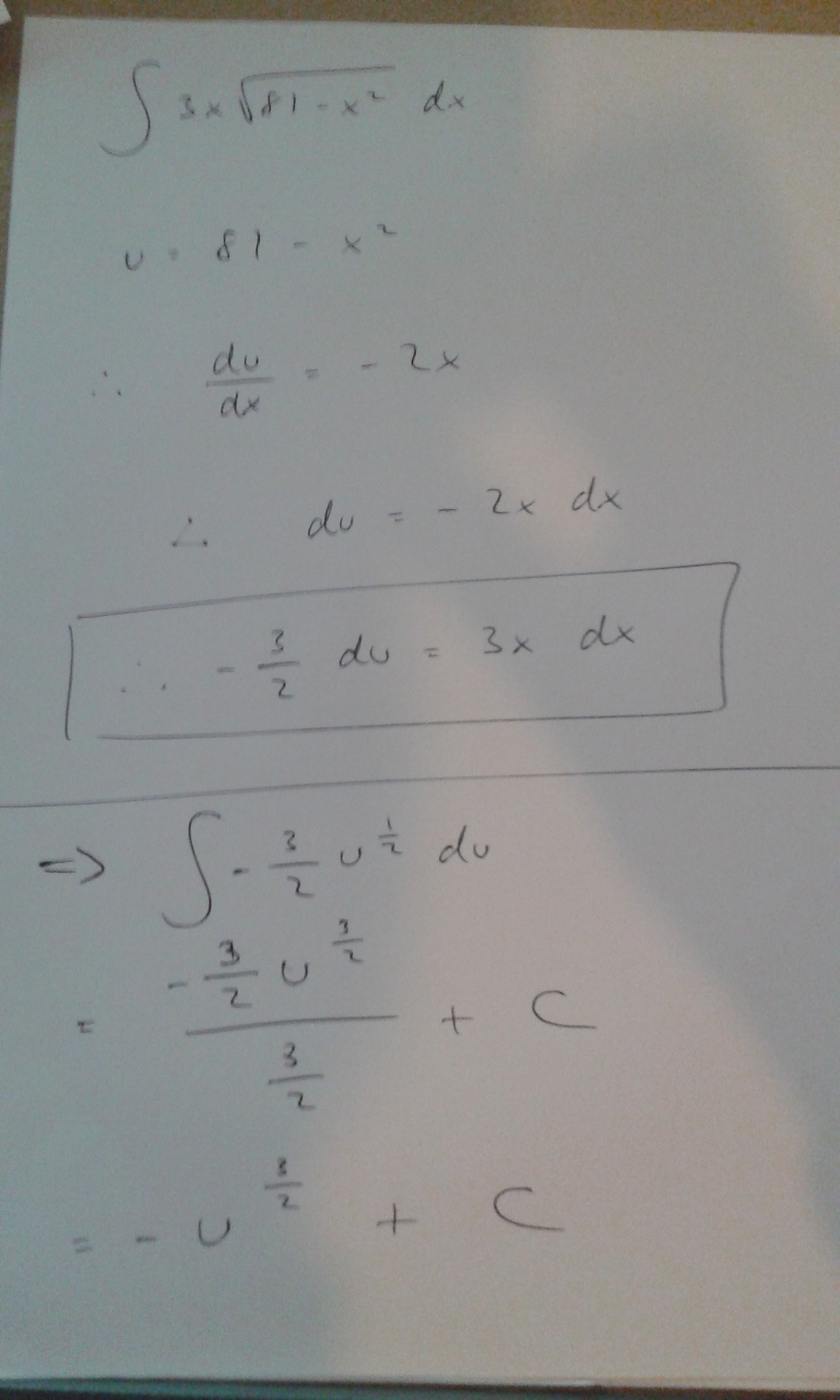
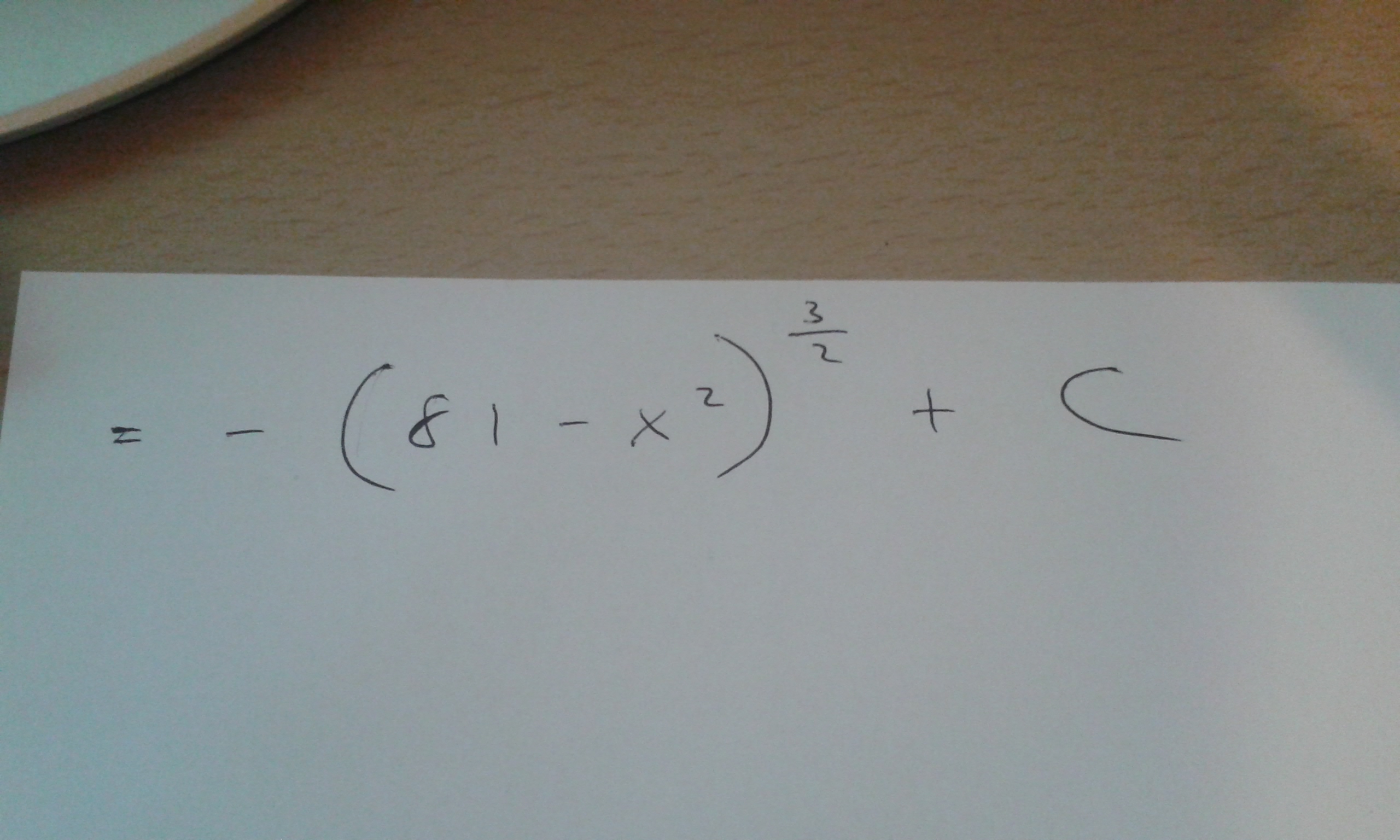
enter image source here

Answer 3 · 2015-04-20T18:54:56

The answer is: #-sqrt((81-x^2)^3)+c#

Remembering that:

#int[f(x)]^n*f'(x)dx=[f(x)]^(n+1)/(n+1)+c#,

than:

#int3xsqrt(81-x^2)dx=-3/2int-2x(81-x^2)^(1/2)dx=#

#=-3/2(81-x^2)^(1/2+1)/(1/2+1)+c=-3/2(81-x^2)^(3/2)/(3/2)+c=#

#=-sqrt((81-x^2)^3)+c#

or, if you want

#=-(81-x^2)sqrt(81-x^2)+c#.