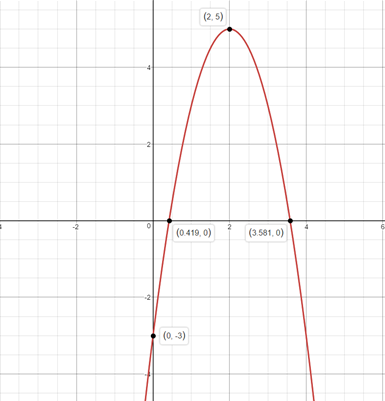
How do you find the intercepts, vertex and graph #f(x)=-2x^2+8x-3#?
1 Answer
Vertex
X intercept
Y-Intercept
Explanation:
Given -
#f(x) = -2x^2+8x-3#
Vertex
#x=(-b)/(2a)=(-8)/(2 xx -2)=8/(-4)=-2#
At
#y=-2(2^2)+8(2)-3#
#y=-8+16-3=16-11=5#
Vertex
X intercept
# -2x^2+8x-3=0#
#x^2-4x+3/2=0# [divide all the terms by#-2# ]
#x^2-4x=-3/2# [Take the constant term to the right]
#x^2-4x+4=-3/2+4# (divide the coefficient of#x# square it and add to both sides]
#x^2-4x+4=-3/2+4=(-3+8)/2=5/2#
#(x-2)^2=-5/2#
#x-2=+-sqrt(5/2)=+-1.58#
#x=1.58+2=3.58#
#x=-1.58+2=0.42#
X intercept
Y-Intercept
At
#y=-2(0)^2+8(0)-3#
#y=-3#
Y-Intercept
To graph the function take a few values on either side of
Find the corresponding
Tabulate them. Graph the pairs