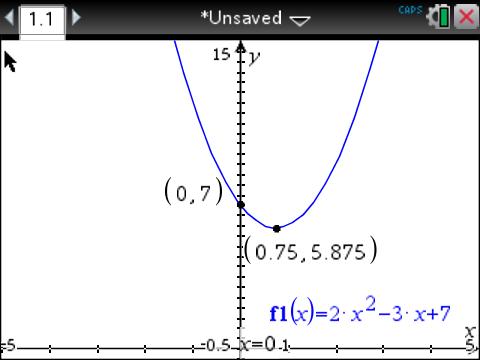
What is the graph of #f(x) = 2x^2 - 3x + 7#?
1 Answer
To graph a quadratic equation we first need to factorise it into a different form.
First we check what the discriminant is equal to
Where
In this case
Because it is less than zero it can't be factored normally
Therefore we must use the The Quadratic Formula or Completing the Square
Here I have completed the square
Remove factor from
Take
Add and then subtract this number inside the equation
Combine the first three terms in a perfect square
Equate left over terms
Multiply coefficient back in
This gives a turning point of
and a