Question

What is the graph of `f(x)=x^2-4x`?

Answer 1

The graph of quadratics of that form is always a parabola.
There are a few things we can tell just from your equation:
1) the leading coefficient is 1, which is positive, so your parabola will open UP.
2) since the parabola opens up, the "end behavior" is both ends up.
3) since the parabola opens up, the graph will have a minimum at its vertex.
Now, let's find the vertex. There are several ways to do this, including using the formula `-b/(2a)` for the x-value.
`(-(-4))/(2*1) = 4/2 = 2`

Substitute x = 2 and find the y-value: `(2)^2-4(2) = 4 - 8 = -4`

The vertex is found at (2, -4).

Here is the graph: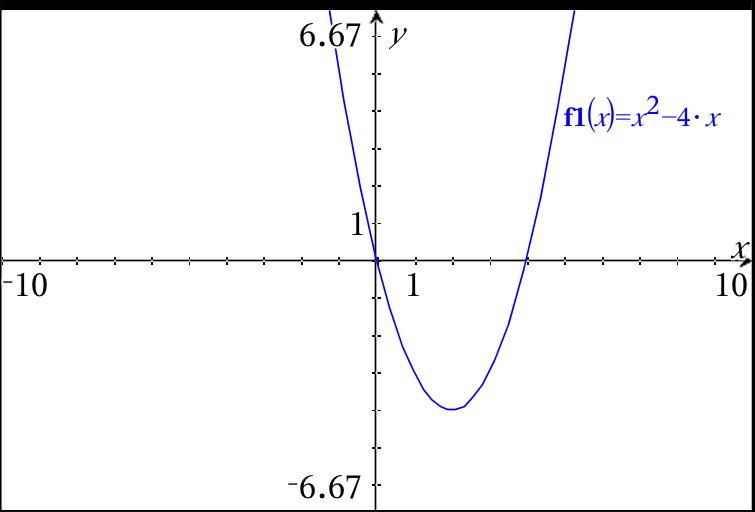

Also, I would suggest factoring the equation to find x-intercepts:
`x(x - 4) = 0` so x = 0 and x = 4. Since the graph has vertical line symmetry through its vertex, you will notice that the vertex is literally halfway between those two x-intercepts, on the vertical line x = 2!

Coincidence? I think not.