How do you find the inverse of # y = | x - 3 |#?

Question

1422 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-17T10:24:59

As scene as below

This is an interesting problem!

I am going to first sketch the function:

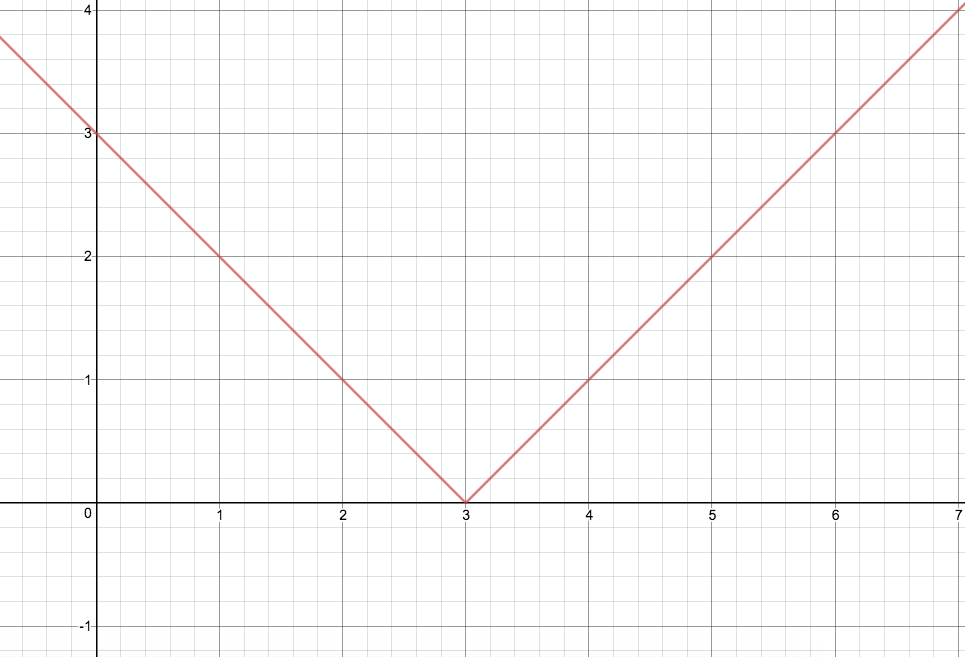
enter image source here

To how we can then say:

#y = x - 3 , x>= 3 #
#y = 3 -x , x<= 3 #

We can now find the inverse of both of these individual graphs:

#y(x) = x-3 #
#=> x = y^-1(x) - 3 #
#=> y^-1(x) = x + 3 #

#y_1(x) = 3 -x #
#=> x = 3- y_1^-1(x)#
#=> y_1^(-1)(x) = 3-x #

Hence the inverse:

#y = 3 - x , x>= 0 #
#y = x +3 , x>= 0 #

We can see that #x>=0# with a sketch of the reflection in #y=x#:

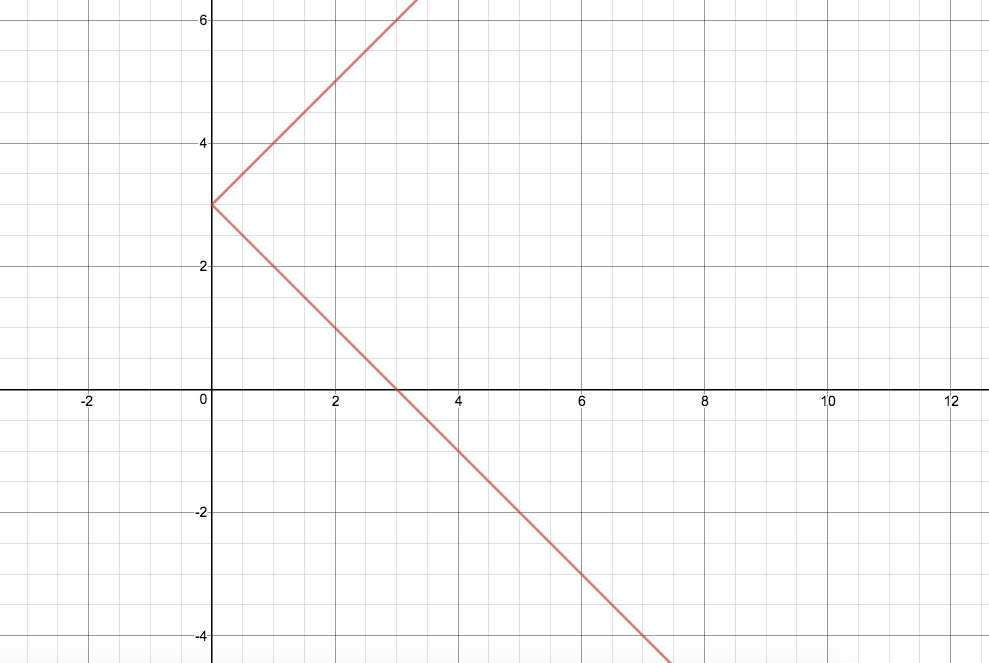
enter image source here

# y = |x-3|# can also be inversed via swappign the #x # for the #y#:

#x = |y-3 |#

Hope this helped you, or at least prompted you in the right direction!