Question

How do you find the length of the diagonal of the rectangle given Side one: 12 in, Side two: 7 in?

Answer 1

Diagonal length `=sqrt(193)`
....See the entire solution process below:

Explanation:

A diagonal across a rectangle forms a right triangle with the sides of the triangle being the sides of the rectangle and the diagonal being the hypotenuse. Therefore we can use the Pythagorean Theorem to solve this problem.

The Pythagorean Theorem states:

`c^2 = a^2 + b^2` where:

`c` is the length of the hypotenuse

`a` and `b` are the lengths of the sides of the right triangle

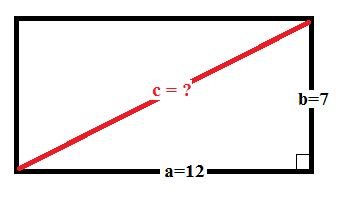
Substituting and calculating `c` gives:

`c^2 = 12^2 + 7^2`

`c^2 = 144 + 49`

`c^2 = 193`

`sqrt(c^2) = sqrt(193)`

`c = sqrt(193) = 13.892`

The length of the diagonal is `sqrt(193)` or `13.892` rounded to the nearest thousandth.