How do you find the length of the missing side given a=19 b=? c=26?

Question

2177 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-03T22:59:59

# b = 17.74#

We need to use the Pythagorean Theorem:

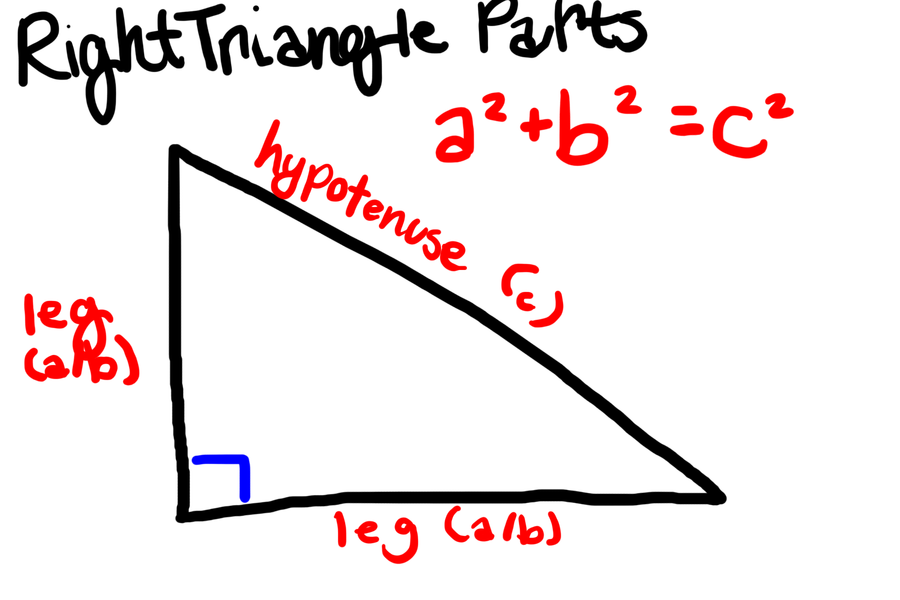
ccancientgreece.tumblr.com

The hypotenuse (c=26) and one of the legs (a=19) are known, so all we have to do is solve for b. We can do that by plugging in our known values:

#19^2+b^2=26^2#

#19^2# or #19xx19# = 361
#26^2# or #26xx26# = 676

Thus, #361+b^2=676#. Now subtract 361 from both sides of the equation to get #b^2# by itself:

#361+b^2=676#
-361 -361

You should end up with:

#b^2=315#

Next, take the square root of both sides to find b. The square root
(#sqrt#) is the inverse of the square (#b^2#)

#sqrt (b^2) = sqrt315#

Therefore, b = 17.74

You can check your answer by plugging a and c into the equation and solve for b to see if your answer matches the given value of b:

#19^2+17.74^2=26^2#