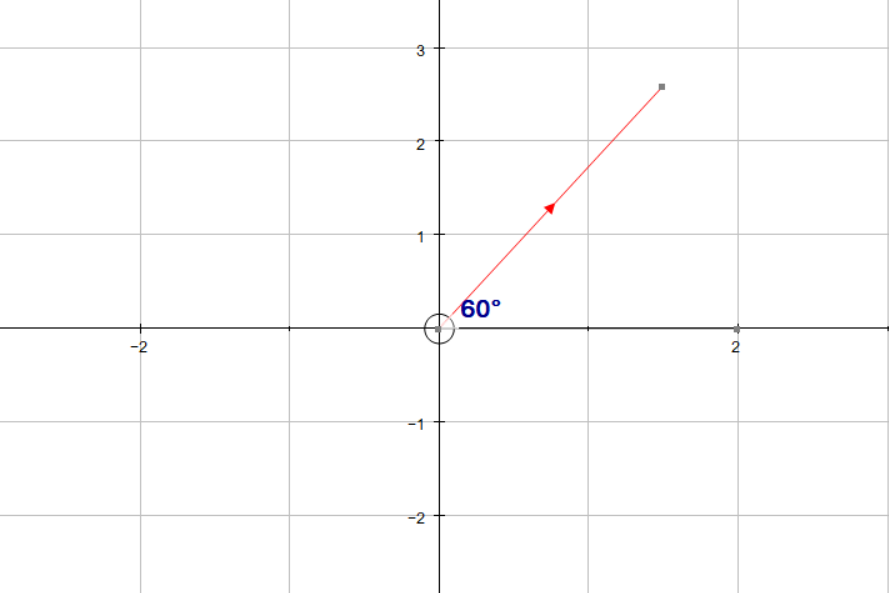
How do you find the magnitude and direction angle of the vector #v=3(cos60i+sin60j)#?

Question

7080 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-26T15:14:21

#3#
#60^o# or #pi/3# radians

To find the magnitude we use a similar idea as used to find the distance between two points.

Magnitude is:

For vector #ul(c)# with component vectors #ai# and #bj#

#|c|= sqrt((ai)^2+(bj)^2#

#3cos(60)= 3/2#

#3sin(60)=(3sqrt(3))/2#

#|v|=sqrt((3/2)^2+((3sqrt(3))/2)^2) = sqrt(9/4+27/4)=+-sqrt(9)=3 , -3#
( negative root not applicable)

So:

#|v|=3#

The direction is the angle formed between the vector and the x axis.

So we find the tangent ratio, which is:

#tan(theta)=(3sin(60))/(3cos(60))=(sin(60))/(cos(60))=((sqrt(3))/2)/(1/2)=sqrt(3)#

#arctan(sqrt(3))= 60^o# or #pi/3# radians

enter image source here