Direction Angles
Key Questions
-
Well, if you look at the name itself you'll guess it...DIRECTION this is the point!!!
You may know that we can use special quantities that are represented by VECTORS. An example of this is VELOCITY.
Velocity has a magnitude, for example 23 km/h, but also direction!!!
Direction is the line along which your vector is applied!
One thing is to say 23 km/h, a better way is to say 23 km/h towards NORTH.So, with vectors you must also specify the direction, not only the magnitude.
Formally, to do that you use the angles the vector forms with the axes. You will now say: 23 km/h at 30° with the x axis.In two dimensions you have the angles
#alpha# and#beta# .
Using trigonometry and Pitagora's Theorem (to evaluate the "length" of your vector) you have: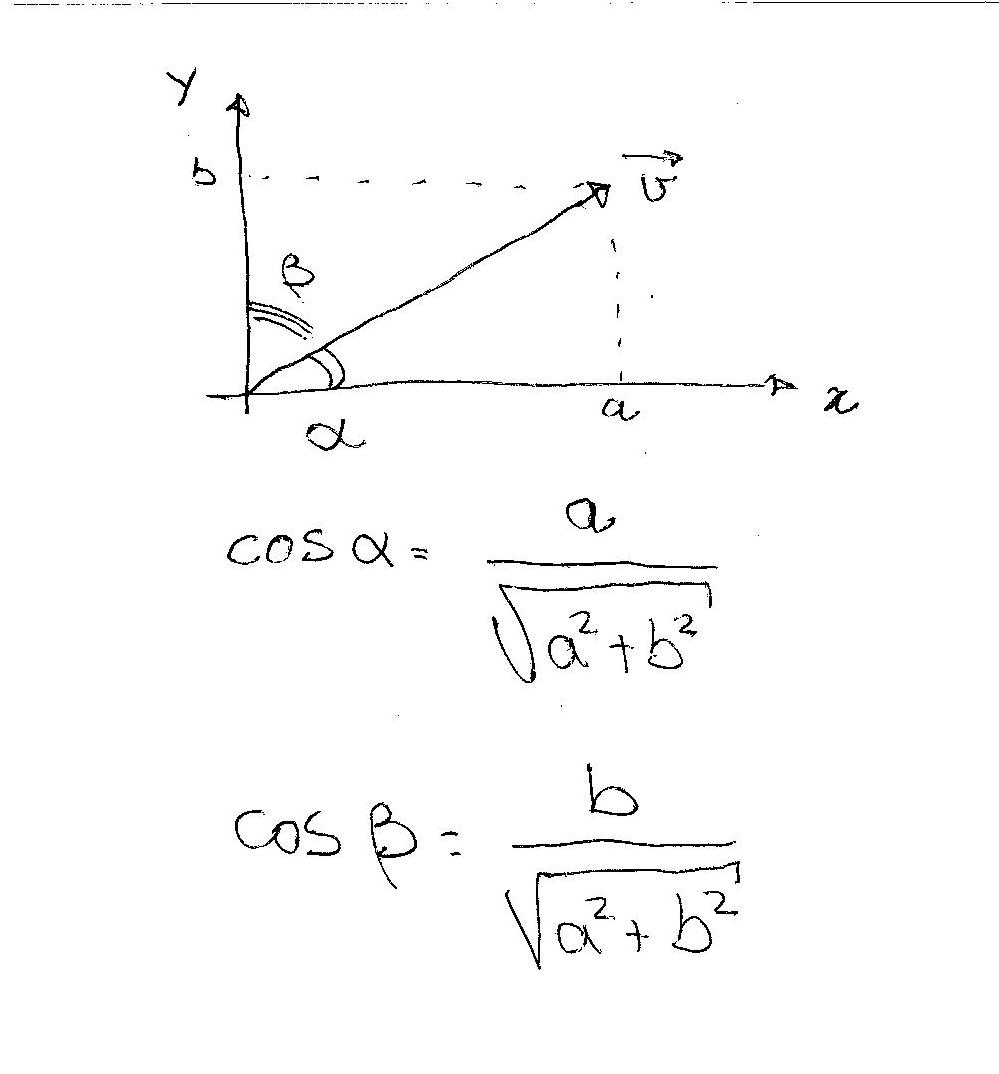
In three dimensions you'll have 3 angles:#alpha, beta and gamma# (and an additional coordinate#c# ).
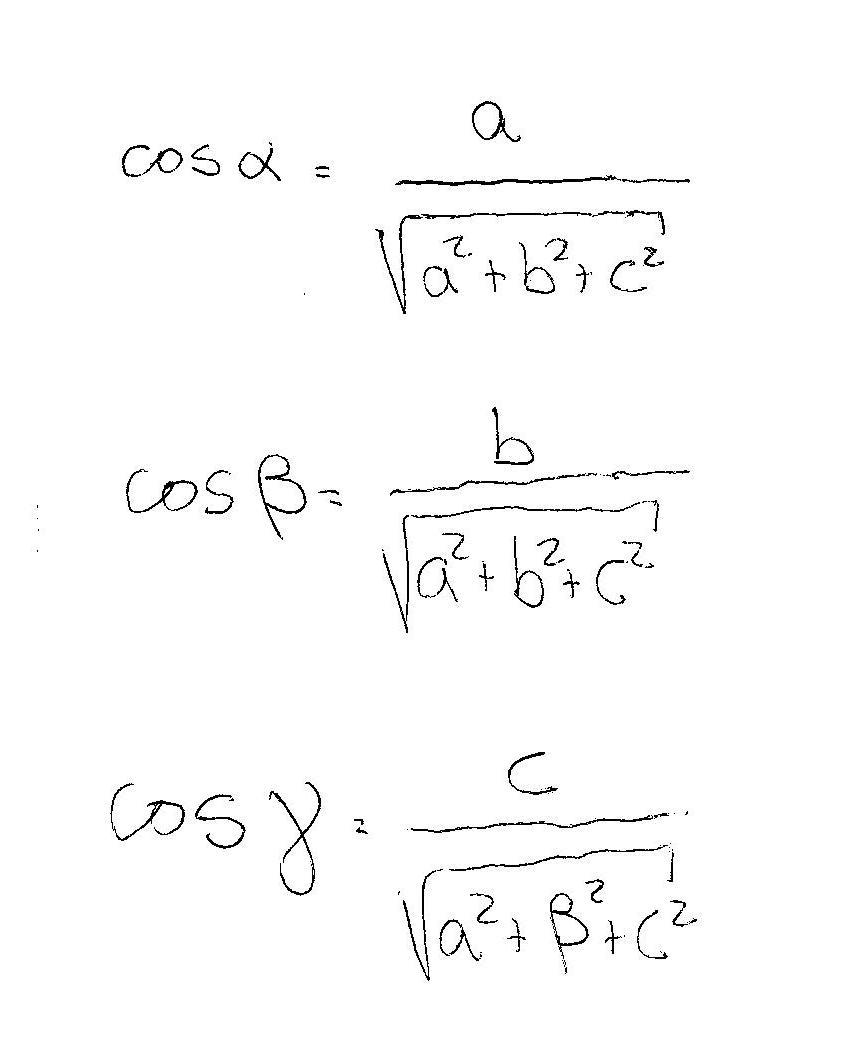
-
Direction angles specify the orientation of the given vector with respect to the x - axis.