To find the magnitude, or length, of a vector, take the square root of the sum of the squares of each component.
#|vecv|=sqrt((veci)^2+(vecj)^2)#
I will explain where this formula comes from below, if you are interested.
Given the vector #vecv=6i-6j# (equivalent to #< 6, -6># ),
#|vecv|=sqrt((6)^2+(-6)^2)#
#=>|vecv|=sqrt(72)#
#=>6sqrt2#
To find the direction angle, use the arctangent (#tan^-1#). You can think of the #i# and #j# components as #x# and #y# components. This will be further explained below as well.
#tan(theta)=y/x#
#=>theta=arctan(y/x)#
#=>theta=arctan(-6/6)#
#=>theta=arctan(-1)#
#=>theta=-pi/4=-45^o#
So the vector has magnitude #6sqrt2# at an angle of #45^o# below the horizontal (or #+x# axis, #-45^o#, etc.).
Further explained:
The formula used above to find the magnitude of the vector comes from Pythagorean theorem.
If we were to graph the vector <6,-6>, we would draw an arrow from the origin to the point (6,-6). This is equivalent to moving #6# units in the positive #i# or #x# direction and #6# units in the negative #j# or #y# direction. Note that we could draw the vector from any point and still end up with the same magnitude and angle.
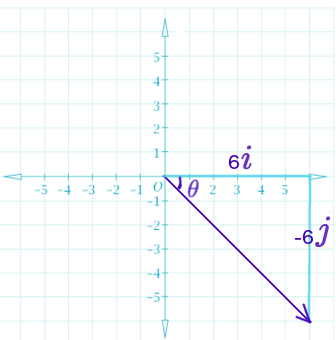
As you can see from the above graph, we can use the #i# and #j# components of the vector to find its length, or magnitude, using the Pythagorean theorem (#a^2+b^2=c^2#), just as we would with any right triangle. We can also see that the #j# component of the vector is opposite #theta#, and the #i# component is adjacent, leading us to use the tangent #=># arctangent to calculate the angle.
Hope this helps!


