How do you find the product of #(a+5)(a-6)#?
2 Answers
Explanation:
To solve this, we expand/distribute using FOIL:
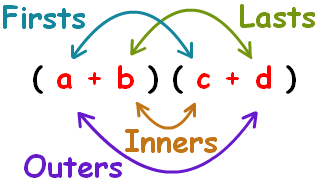
As you can see in this image, the first thing we do is multiply the
Then the
Then the
and finally the
Now combine them all together:
We can still simplify the like terms. Let's color-code them:
Combine like terms and get the final answer:
Hope this helps!
Explanation:
Multiply everything in the right brackets (green) by everything in the left brackets (blue).
Notice that the + sign followed the 5
but


