How do you find the product of #(t+2)(t+9)#?

Question

1117 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-20T05:12:10

#t^2 + 11t + 18#

Here's how I did it:

#(t+2)(t+9)#

To simplify this, we will use the distributive method called FOIL:
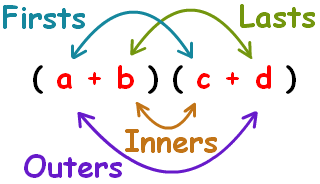
enter image source here

Following this image, we can multiply it out.

The #color(teal)("firsts")#:
#color(teal)(t*t) = t^2#

The #color(indigo)("outers")#:
#color(indigo)(t*9) = 9t#

The #color(peru)"inners"#:
#color(peru)(2*t) = 2t#

The #color(olivedrab)"lasts"#:
#color(olivedrab)(2*9) = 18#

Combine them all together to get your answer:
#t^2 + 9t + 2t + 18#

We can still combine the like terms #9t# and #2t#, so the final simplification is:
#t^2 + 11t + 18#

Hope this helps!