Question

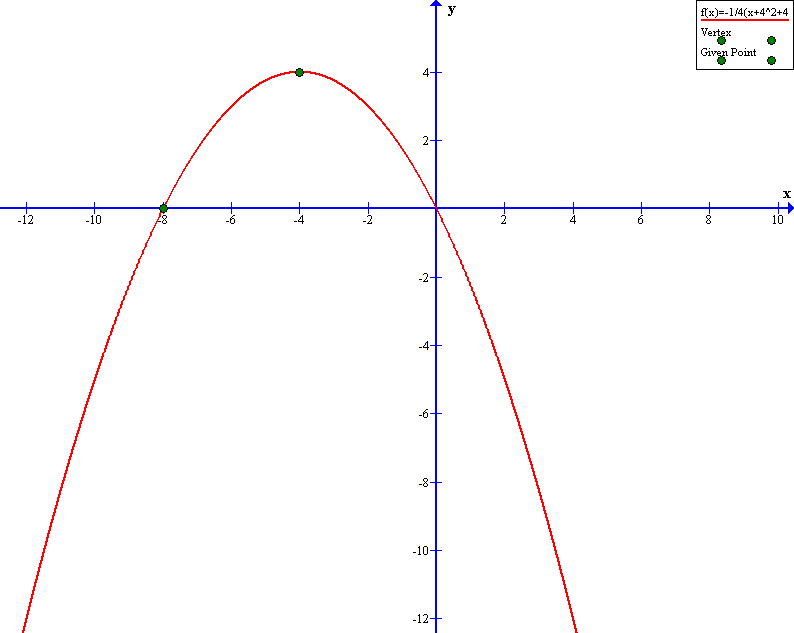
How do you find the quadratic function `y=f(x)` whose graph has a vertex `(-4,4)` and passes through the point `(-8,0)`?

Write the function in standard form.

Answer 1

`f(x)=-1/4(x+4)^2+4`

Explanation:

The general vertex form for a parabola with vertex at `(color(red)a,color(blue)b)` is
`color(white)("XXX")f(x)=color(green)m(x-color(red)a)^2+color(blue)b`
(you can simplistically think of `color(green)m` as being an indication of the "spread" of the parabola).

Given the vertex `(color(red)(-4),color(blue)4)`
we have
`color(white)("XXX")f(x)=color(green)m(x+4)^2+4`

We are told that `(x,f(x))=(color(magenta)(-8),color(cyan)0)` is a solution for this equation
`color(white)("XXX")color(cyan)0=m(color(magenta)(-8)+4)^2+4`

`color(white)("XXX")rarr 0= 16m+4`

`color(white)("XXX")rarr m= -1/4`

and the required parabolic equation is
`color(white)("XXX")f(x)=-1/4(x+4)^2+4`

Here is the graph for verification: