Identify Critical Points
Key Questions
-
Since the equation for a parabola describe a quadratic function
#y=ax^2+bx+c# ,where
#a# ,#b# , and#c# are any real numbers such that#a ne 0# ,we can find the x-intercepts by solving the quadratic equation
#ax^2+bx+c=0# .One way to do that, we can use the quadratic formula
#x={-b pm sqrt{b^2-4ac}}/{2a}# .
I hope that this was helpful.
-
If given a graph: the y-intercept passes through y-axis.
Example:
If a graph passes the y-axis at -1, then the y-intercept is -1.If you can not see the y-axis, you need to chose two points and create the equation of the parabola in standard or vertex form (using vertex and another point).
Example on how to create an equation from the graph of the parabola (when y-axis cannot be seen):
Vertex: (3,4)
Point: (5, -4)
-4 =#a(5-3)^2# +4
-4 =#a(2)^2# + 4
-4 =#a(4)# + 4
-4 = 4a + 4
-4 - 4 = 4a
-8 = 4a
#-8/4# =#(4a)/4#
-2 = a
Equation: y =#-2(x-3)^2# +4 (refer below to find the y-intercept)If an equation: When a point is on the y-axis, the x value is 0. Therefore it you want to plug in 0 for your x values. y =
#ax^2# + bx + c, has a y-intercept at c.Example (vertex Form y =
#a(x-h)^2# +k ):
y =#3(x-4)^2# + 5
y =#3(0-4)^2# + 5
y =#3(-4)^2# + 5
y = 3(16) +5
y = 48 + 5
y = 53
Y-intercept is 53Example (Standard Form y =
#ax^2# + bx + c):
y =#2x^2# -3x + 4
y =#2(0)^2# -3(0) + 4
y = 2(0) - 3(0) + 4
y = 0 - 0 + 4
y = 4 (the c value)
Y-intercept is 4 -
The same way you tell if a parabola opens up or down, by the leading coefficient of the variable.
Since the
#x# -axis is positive to the right, a positive leading coefficient (3) means it opens to the right. eg.#y=+-sqrt(3x-4)+3# And a negative leading coefficient (-2) means it opens to the left.
#y=+-sqrt(4-2x)+2# 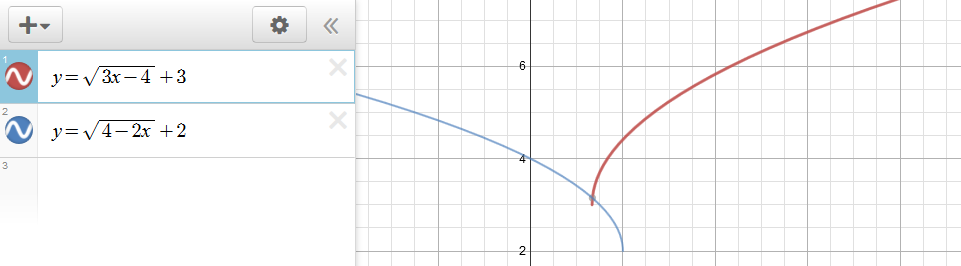
Note that only the top halves of the parabolas are drawn.