#-515# is no the simplest form for this angle.
See, #900# degrees is the same angle as #180# degrees, and one of the ways I like to check that that's true -- if I have a calculator handy --is to plug in #sin(180)# and #sin(900)#, and if they are the same angle, they'll give me the same answer. And they do, #0# for both of them.
Let's try and find the simplified angle for #-515#. Now, that negative might look scary, but it just means that the angle was found by going clockwise, unlike the normal way where we move counter-clockwise.
So we'll ignore the negative sign for now. The first thing I do is imagine drawing a line all the way around the circle
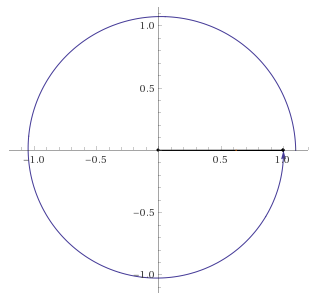
That used up #360# degrees. Now we have #115# degrees left
Now I move another #90# degrees
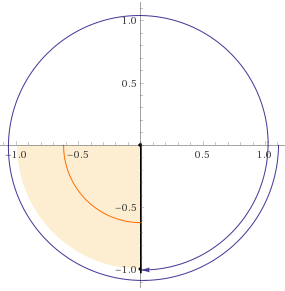
Now I have #65# degrees left
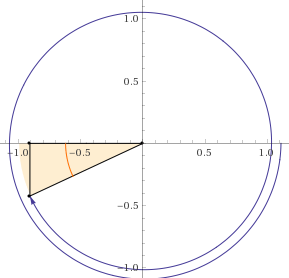
Now we can look at the final picture and see how many degrees it would take to reach this angle, but going in a clockwise direction . That'll give us our reference angle
So, we'll need to go #180# degrees. And we know that we used up #65# degrees, so there are #25# degrees left in that qudarant. #180 + 25# gives us #205#
So, we are saying that #205# and #-515# are two different ways to reference the same angle. Let;s plug them into #sin(theta)# and find out!
#sin(205) = -0.4226#
#sin(-515) = -0.4226#
Yep! The reference angle for #-515# is #205#

