How do you find the right triangle of maximum area if the sum of the lengths of the legs is 3?
1 Answer
Jun 3, 2015
We know that
Let's use substitution and replace
The maximum area can be found by studying the sign of the derivative of the area :
The derivative
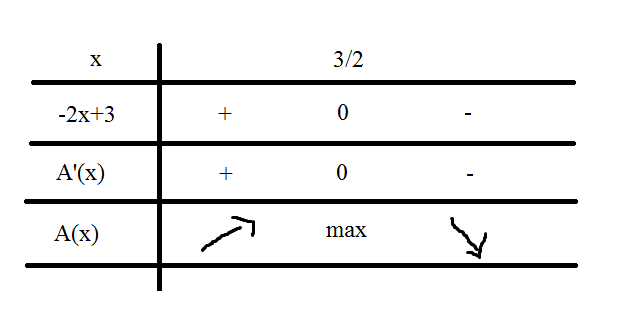
Therefore, the area is maximal when

