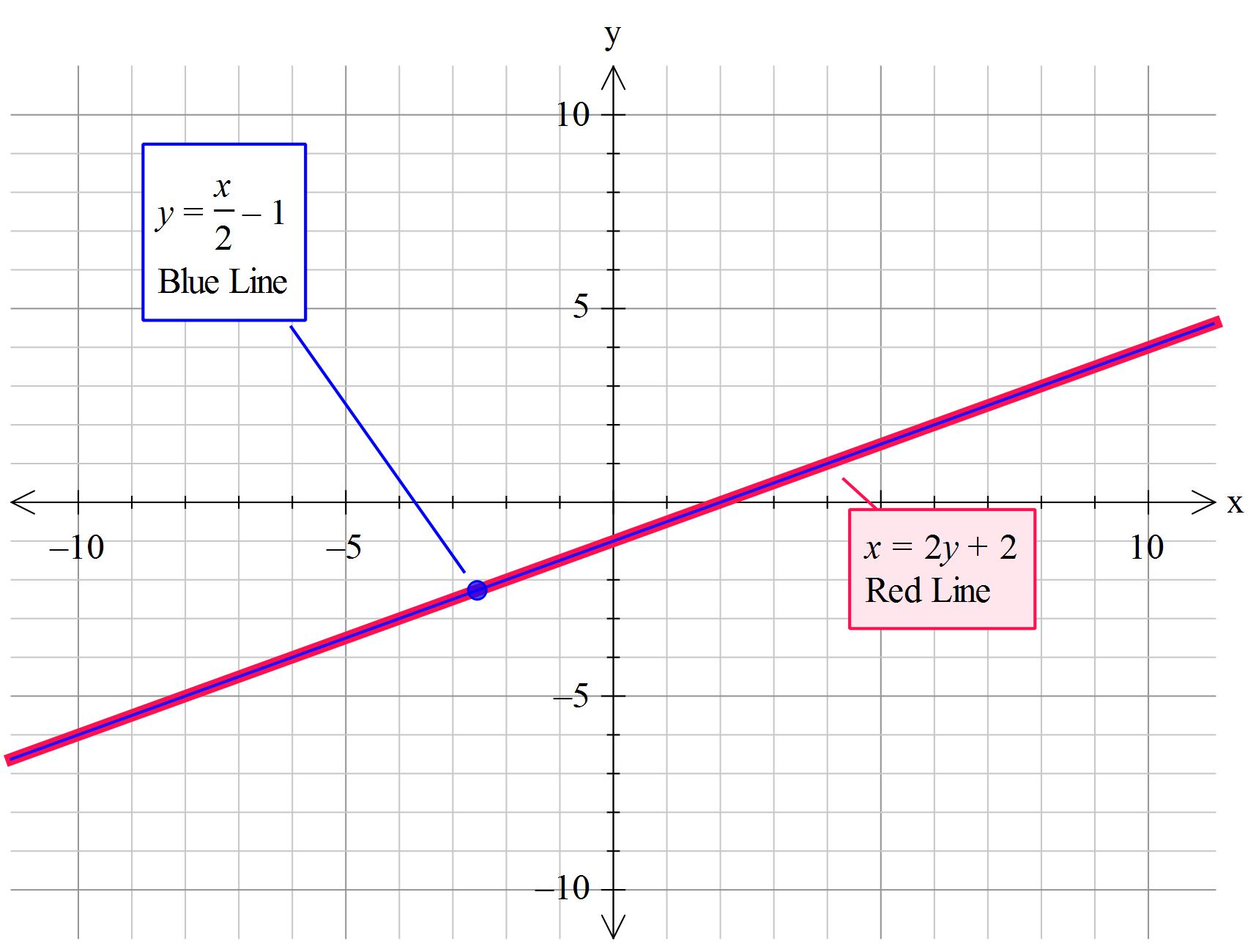
#color(brown)("It does not matter if you have "x=2y+2" or by ")#
#color(brown)("manipulation "y=x/2-1 ". They both plot the same ")##color(brown)("straight line.")#
So the slope #color(blue)("(gradient) is 2")#. That is: for every 1 along you go up 2. You always read from left to right for the gradient.
+2 means the line goes up whilst -2 means it goes down!
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("To determine "x_("intercept"))#
The line will cross the x-axis at y=0
Set y=0 giving:
#x=2(0)+2#
#color(blue)(x_("intercept")=2)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("To determine "y_("intercept"))#
The line will cross the y-axis at x=0
Set x=0 giving:
#0=2y+2#
Subtract #color(red)( 2)# from both sides
#0color(red)(-2)=2y+2color(red)(-2)#
#-2=2y+0#
Divide both sides by #color(red)(2)#
#-2/(color(red)(2))=2/(color(red)(2)) xx y#
But #2/(-2)=-1" and "2/2=+1#
#-1=1xxy#
#color(blue)(y_("intercept")=-1)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~