Question

How do you find the slope of the line parallel to and perpendicular to `2y-x=7`?

Answer 1

The equation of the line parallel to the given line is -

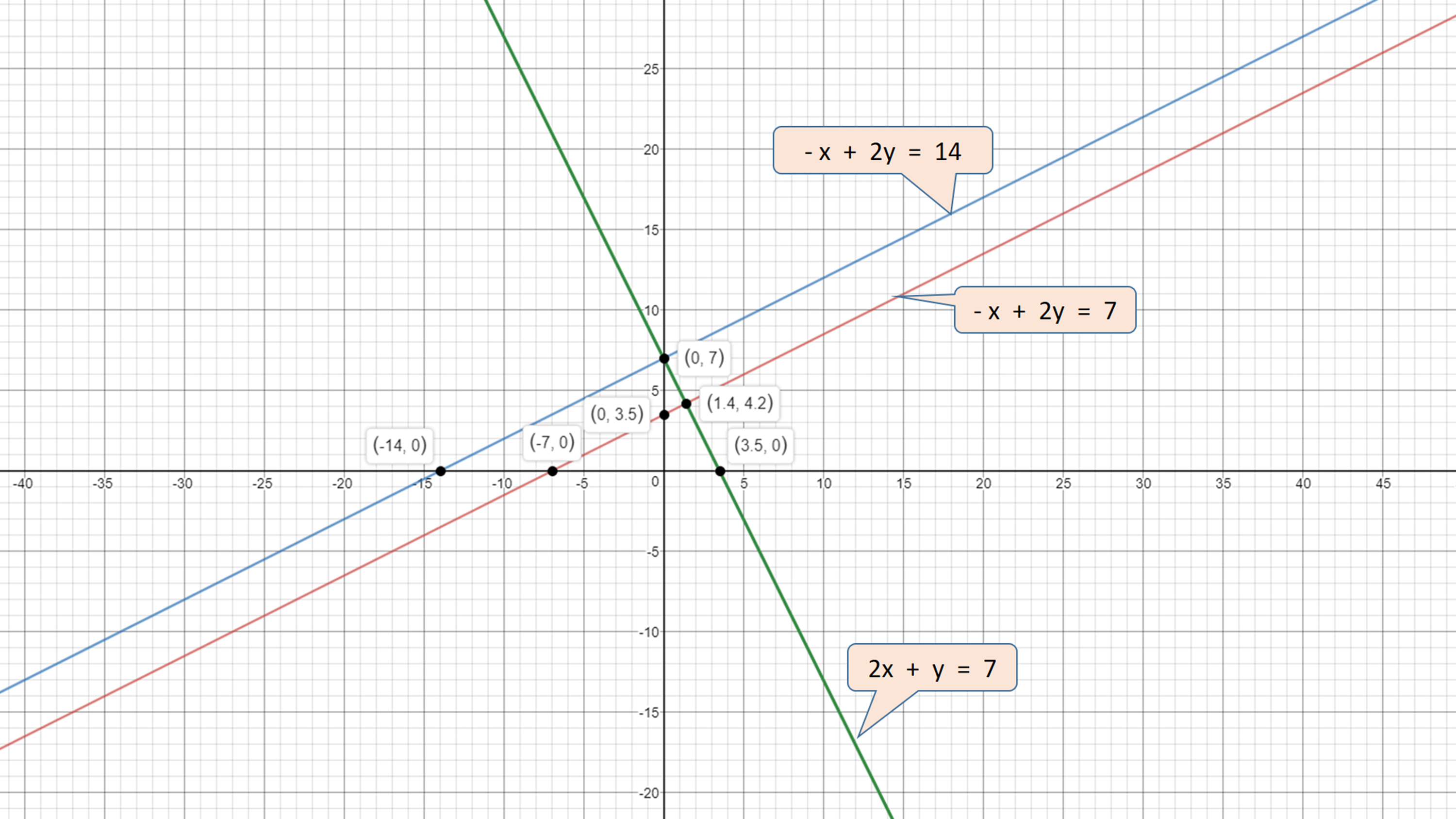
`-x+2y=14`
The equation of the perpendicular line is -
`2x+y=7`

Explanation:

Given -

`2y-x=7`

Rewrite it as to suit our convenience.

`-x+2y=7`

The slope of the line is given by the formula

`m=(-a)/b`

Where -

`a-` is the coefficient of x
`b-` is the coefficient of y

The slope of the given line `m_1=(-a)/b=(-(-1))/2=1/2`

For a line to be parallel, it also must have the same slope.

So it is enough if you change the value of the Constant term.

Let us replace 7 with 14. There is no hard and fast rule in assigning any other value. A line can have any number of parallel lines.

The equation of the line parallel to the given line is -

`-x+2y=14`

For a line to be perpendicular, the product of the slopes of the two lines must be equal to `m_1xxm_2=-1`

There is short cut to find the equation of a perpendicular line.

Step 1
Interchange the coefficients of `x` and `y`

`2x-1y=7`

Step 2

Change the sign of the `y` coefficient

`2x+1y=7`

Now write the equation

The equation of the perpendicular line is -

`2x+y=7`

Its slope is `m_2=2/1=2`

Find the product to acertain the correctness of your answer

`m_1 xx m_2=(-1)/2xx2=-1`

Hence the equation of the perpendicular line is correct.