How do you find the slope that is perpendicular to the line 2x +3y = 5?
1 Answer
Take the negative reciprocal of the given line's slope. The new slope will be
Explanation:
Lines that are perpendicular will have negative reciprocal slopes. Meaning, if one line's slope is
Why? A line's slope is equal to its rise over its run—also written as
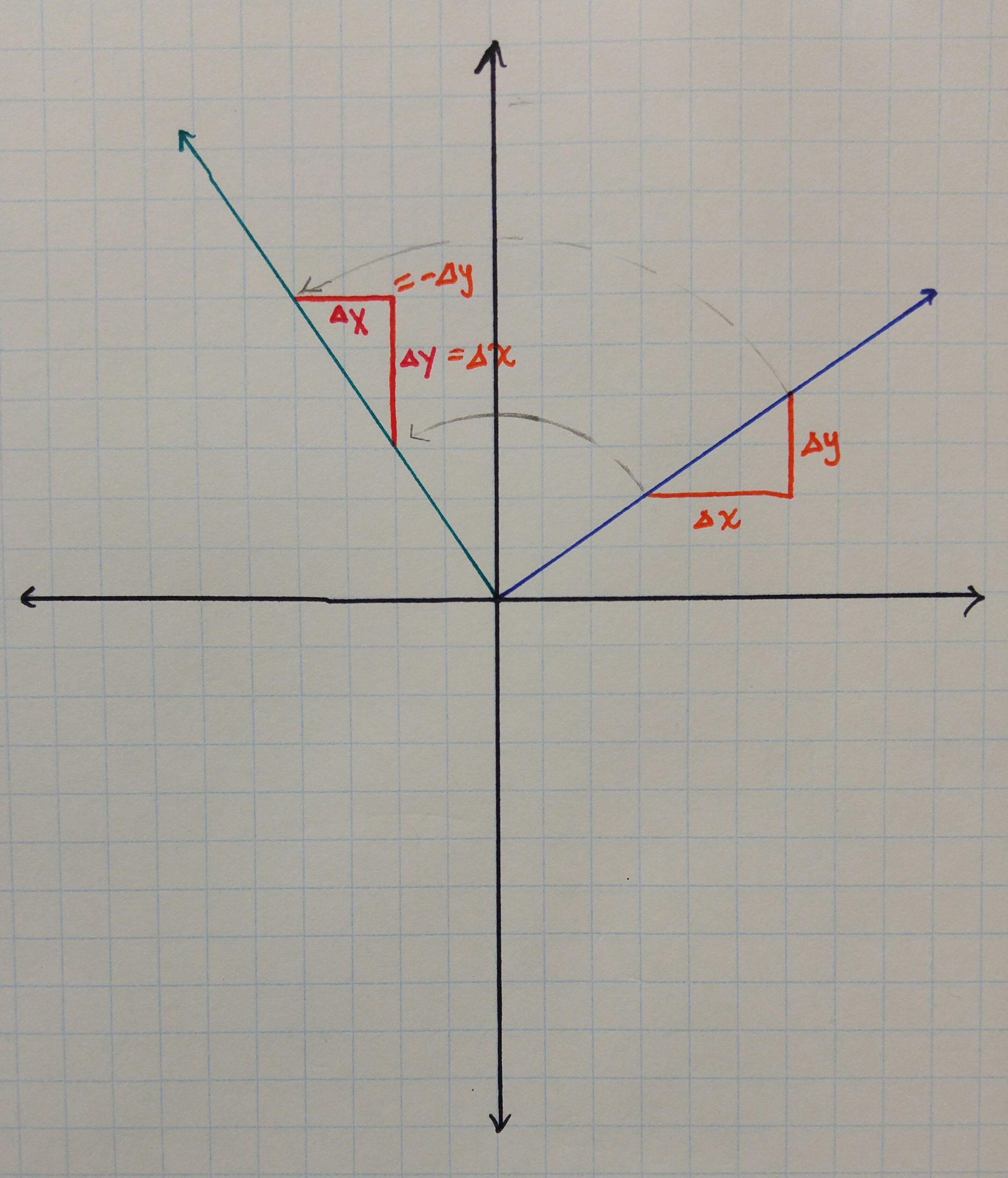
In math terms:
Delta y_"new"=Delta x" "and" "Delta x_"new" = -Delta y
thus
m_"new"=(Delta y_"new")/(Delta x_"new")=(Delta x)/(-Delta y)=-(Delta x)/(Delta y)=-1/m
(Note: if we rotate this new line another 90° (180° total from the beginning), this 3rd line will have a slope of
Okay, great—so what's the slope of
y=-2/3 x+5/3 ,
meaning that for every step of "2 down", we have a step of "3 right".
The negative reciprocal of the slope
m_"new"=-1/m=(-1)/(- 2/3)=3/2 ,
meaning that, for a perpendicular line, a step of "3 up" comes with a step of "2 right".

